Đề số 5 - Đề thi vào lớp 10 môn Toán

Câu 1. 

1. Thực hiện phép tính \(\dfrac{{\sqrt {27} }}{{\sqrt 3 }}\)

2. Rút gọn biểu thức \(P = \left( {\dfrac{{\sqrt x }}{{3 + \sqrt x }} + \dfrac{{9 + x}}{{9 - x}}} \right).\left( {3\sqrt x  - x} \right)\)  với \(x \ge 0\)  và \(x \ne 9\)

3. Xác định các hệ số a, b để đồ thị hàm số \(y = ax + b\)  đi qua hai điểm  \(A\left( {2; - 2} \right)\) và \(B\left( { - 3;2} \right)\)

Câu 2. 

1. Giải phương trình \({x^2} - 4x + 4 = 0\)

2. Tìm giá trị của m để phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3 = 0\) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(\left| {{x_1}} \right| + \left| {{x_2}} \right| = 10.\)

Câu 3. Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:

Một xe ô tô đi từ A đến B theo đường quốc lộ cũ dài 156 km với vận tốc không đổi. Khi từ B về A, xe đi đường cao tốc mới nên quãng đường giảm được 36 km so với lúc đi và vận tốc tăng so với lúc đi là 32 km/h. Tính vận tốc ô tô khi đi từ A đến B, biết thời gian đi nhiều hơn thời gian về là 1 giờ 45 phút.

Câu 4. 

Cho đường tròn tâm O, đường kính AB = 2R. Trên đường tròn (O) lấy điểm C bất kì (C không trùng với A và B). Tiếp tuyến của đường tròn (O) tại A cắt tia BC ở điểm D. Gọi H là hình chiếu của A trên đường thẳng DO. Tia AH cắt đường tròn (O) tại điểm F (không trùng với A). Chứng minh

a) \(D{A^2} = DC.DB\)

b) Tứ giác AHCD nội tiếp.

c) \(CH \bot CF\)

d) \(\dfrac{{BH.BC}}{{BF}} = 2R\)

Câu 5 

Cho x, y là các số thực dương thỏa mãn \(xy + 1 \le x\). Tìm giá trị nhỏ nhất của biểu thức \(Q = \dfrac{{x + y}}{{\sqrt {3{x^2} - xy + {y^2}} }}\)

Câu 1.

1. Thực hiện phép tính \(\dfrac{{\sqrt {27} }}{{\sqrt 3 }}\)

\(\dfrac{{\sqrt {27} }}{{\sqrt 3 }} = \sqrt {\dfrac{{27}}{3}}  = \sqrt 9  = 3.\)

2. Rút gọn biểu thức \(P = \left( {\dfrac{{\sqrt x }}{{3 + \sqrt x }} + \dfrac{{9 + x}}{{9 - x}}} \right).\left( {3\sqrt x  - x} \right)\)  với \(x \ge 0\)  và \(x \ne 9\)

Điều kiện: \(x \ge 0,\;\;x \ne 9.\)

\(\begin{array}{l}P = \left( {\dfrac{{\sqrt x }}{{3 + \sqrt x }} + \dfrac{{9 + x}}{{9 - x}}} \right).\left( {3\sqrt x  - x} \right)\\\;\;\; = \left( {\dfrac{{\sqrt x .\left( {3 - \sqrt x } \right)}}{{\left( {3 - \sqrt x } \right)\left( {3 + \sqrt x } \right)}} + \dfrac{{9 + x}}{{\left( {3 - \sqrt x } \right)\left( {3 + \sqrt x } \right)}}} \right).\left( {3\sqrt x  - x} \right)\\\;\;\; = \dfrac{{9 + 3\sqrt x }}{{\left( {3 - \sqrt x } \right)\left( {3 + \sqrt x } \right)}}.\left( {3\sqrt x  - x} \right)\\\;\;\; = \dfrac{{3\left( {3 + \sqrt x } \right)}}{{3 + \sqrt x }}.\sqrt x \\\;\;\; = 3\sqrt x .\end{array}\)

3. Xác định các hệ số a, b để đồ thị hàm số \(y = ax + b\)  đi qua hai điểm  \(A\left( {2; - 2} \right)\) và \(B\left( { - 3;2} \right)\)

Đồ thị hàm số \(y = ax + b\)  đi qua hai điểm  \(A\left( {2; - 2} \right)\) và \(B\left( { - 3;2} \right)\) nên ta có hệ phương trình:

\(\left\{ \begin{array}{l}2a + b =  - 2\\ - 3a + b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5a =  - 4\\b = 2 + 3a\end{array} \right. \)

\(\Leftrightarrow \left\{ \begin{array}{l}a =  - \dfrac{4}{5}\\b =  - \dfrac{2}{5}\end{array} \right.\)

Vậy ta có \(a =  - \dfrac{4}{5};\;\;b =  - \dfrac{2}{5}.\)

Câu 2.

1. Giải phương trình \({x^2} - 4x + 4 = 0\)

\({x^2} - 4x + 4 = 0\)

\(\Leftrightarrow {\left( {x - 2} \right)^2} = 0 \Leftrightarrow x = 2\)

2. Tìm giá trị của m để phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3 = 0\) (*) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(\left| {{x_1}} \right| + \left| {{x_2}} \right| = 10\)

+) Phương trình có hai nghiệm \({x_1},{x_2}\) khi và chỉ khi \(\Delta ' \ge 0 \Leftrightarrow {\left( {m + 1} \right)^2} - {m^2} - 3 \ge 0\)

\(\Leftrightarrow {m^2} + 2m + 1 - {m^2} - 3 \ge 0 \)

\(\Leftrightarrow 2m \ge 2 \Leftrightarrow m \ge 1.\)

Áp dụng hệ thức Vi-et cho phương trình (*) ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m + 1} \right)\,\,\left( 2 \right)\\{x_1}{x_2} = {m^2} + 3\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)\end{array} \right.\)

Từ đề bài ta có: \(\left| {{x_1}} \right| + \left| {{x_2}} \right| = 10 \)

\(\Leftrightarrow x_1^2 + x_2^2 + 2\left| {{x_1}{x_2}} \right| = 100\)

\(\Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} + 2\left| {{x_1}{x_2}} \right| = 100\)

Lại có \({x_1}{x_2} = {m^2} + 3 > 0\;\forall m \) \(\Rightarrow \left| {{x_1}{x_2}} \right| = {x_1}{x_2} = {m^2} + 3.\)

Khi đó ta có: \(\left| {{x_1}} \right| + \left| {{x_2}} \right| = 10\)

\(\Leftrightarrow {\left( {\left| {{x_1}} \right| + \left| {{x_2}} \right|} \right)^2} = 100\)

\(\begin{array}{l} \Leftrightarrow x_1^2 + 2\left| {{x_1}{x_2}} \right| + x_2^2 = 100\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} + 2{x_1}{x_2} = 100\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} = 100\\ \Leftrightarrow {x_1} + {x_2} =  \pm 10.\end{array}\)

+) TH1: \({x_1} + {x_2} = 10\) kết hợp với   (2) ta được:

\(\left\{ \begin{array}{l}{x_1} + {x_2} = 10\\{x_1} + {x_2} = 2\left( {m + 1} \right)\end{array} \right. \)\(\,\Leftrightarrow 2\left( {m + 1} \right) = 10 \Leftrightarrow m = 4\left( {tm} \right)\)

+)TH2: \({x_1} + {x_2} = 10\) kết hợp với   (2) ta được:

\(\left\{ \begin{array}{l}{x_1} + {x_2} =  - 10\\{x_1} + {x_2} = 2\left( {m + 1} \right)\end{array} \right. \)\(\,\Leftrightarrow 2\left( {m + 1} \right) =  - 10 \Leftrightarrow m =  - 6\;\left( {ktm} \right)\)

Vậy \(m = 4\) thỏa mãn điều kiện bài toán.

Câu 3:

Một xe ô tô đi từ A đến B theo đường quốc lộ cũ dài 156 km với vận tốc không đổi. Khi từ B về A, xe đi đường cao tốc mới nên quãng đường giảm được 36 km so với lúc đi và vận tốc tăng so với lúc đi là 32 km/h. Tính vận tốc ô tô khi đi từ A đến B, biết thời gian đi nhiều hơn thời gian về là 1 giờ 45 phút.

Gọi vận tốc của ô tô khi đi từ A đến B là \(x\;\left( {km/h} \right)\;\;\left( {x > 0} \right).\)

Thời gian ô tô đi từ A đến B là: \(\dfrac{{156}}{x}\) (giờ).

Quãng đường lúc về là: \(156 - 36 = 120\left( {km} \right)\)

Vận tốc của ô tô lúc về là: \(x + 32\;\;\left( {km/h} \right).\) Thời gian của ô tô lúc về là: \(\dfrac{{120}}{{x + 32}}\) (giờ).

Đổi:  1 giờ 45 phút \( = 1 + \dfrac{{45}}{{60}} = \dfrac{7}{4}\) giờ.

Theo đề bài ta có phương trình: \(\dfrac{{156}}{x} - \dfrac{{120}}{{x + 32}} = \dfrac{7}{4}\)

\(\begin{array}{l} \Leftrightarrow 156.4.\left( {x + 32} \right) - 120.4.x = 7x\left( {x + 32} \right)\\ \Leftrightarrow 624x + 19968 - 480x = 7{x^2} + 224x\\ \Leftrightarrow 7{x^2} + 80x - 19968 = 0\\ \Leftrightarrow \left( {x - 48} \right)\left( {7x + 416} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 48 = 0\\7x + 416 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 48\;\;\left( {tm} \right)\\x =  - \dfrac{{416}}{7}\;\;\left( {ktm} \right)\end{array} \right..\end{array}\)

Vậy vận tốc của ô tô lúc đi từ A đến B là \(48\;km/h.\)

Câu 4.

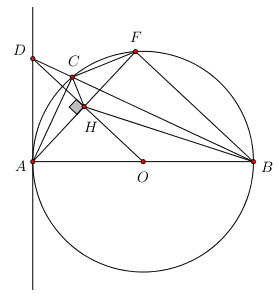
a) \(D{A^2} = DC.DB\)

Ta có \(\) (góc nội tiếp chắn nửa đường tròn tâm O) \( \Rightarrow AC \bot BC\,\,hay\,\,\,AC \bot BD\).

Ta có:\(\widehat {DAB} = {90^0}\) ( Do DA là tiếp tuyến của đường tròn tâm O tại A).

Áp dụng hệ thức lượng trong tam giác vuông ABD vuông tại A có đường cao AC ta có \(D{A^2} = DC.DB\).

b) Tứ giác AHCD nội tiếp.

Xét tứ giác AHCD có \(\widehat {AHD} = \widehat {ACD} = {90^0} \Rightarrow \) Hai đỉnh C và H kề nhau cùng nhìn cạnh AD dưới góc 90⁰

\( \Rightarrow \) Tứ giác AHCD nội tiếp (Tứ giác có hai đỉnh kề nhau cùng nhìn 1 cạnh dưới các góc bằng nhau).

c) \(CH \bot CF\)

Do tứ giác AHCD nội tiếp nên \(\widehat {FHC} = \widehat {ADC}\) (cùng bù với \(\widehat {AHC}\)).

Xét tam giác FHC và tam giác ADC có:

\(\widehat {CFH} = \widehat {DAC}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AC).

\(\widehat {FHC} = \widehat {ADC}\,\,\left( {cmt} \right)\);

Suy ra, tam giác FHC đồng dạng với tam giác ADC (g.g) => góc FCH bằng góc ACD (hai góc tương ứng)

Mà \(\widehat {ACD} = {90^0} \Rightarrow \widehat {FCH} = {90^0} \Rightarrow CH \bot CF\)

d) \(\dfrac{{BH.BC}}{{BF}} = 2R\)

Xét tam giác vuông OAD vuông tại A có OH là đường cao ta  có \(O{A^2} = OD.OH\) (hệ thức lượng trong tam giác vuông)

Mà \(OA = OB = R \Rightarrow O{B^2} = OD.OH \)

\(\Rightarrow \dfrac{{OB}}{{OH}} = \dfrac{{OD}}{{OB}}\)

Xét tam giác OBH và ODB có:

\(\widehat {BOD}\) chung;

\(\dfrac{{OB}}{{OH}} = \dfrac{{OD}}{{OB}}\,\,\left( {cmt} \right)\);

Suy ra, tam giác OBH đồng dạng với tam giác ODB (c.g.c) => góc OBH bằng góc OBD

Mà \(\widehat {ODB} = \widehat {CAF}\) (hai góc nội tiếp cùng chắn cung CH của đường tròn ngoại tiếp tứ giác AHCD).

\(\widehat {CAF} = \widehat {CBF}\) (hai góc nội tiếp cùng chắn cung CF của đường tròn (O))

\( \Rightarrow \widehat {OBH} = \widehat {CBF} \)

\(\Rightarrow \widehat {OBH} + \widehat {HBC} = \widehat {CBF} + \widehat {HBC}\)

\(\Rightarrow \widehat {OBC} = \widehat {HBF} = \widehat {ABC}\)

Xét tam giác BHF và tam giác BAC có:

\(\widehat {BFH} = \widehat {BCA} = {90^0}\) (góc BFC nội tiếp chắn nửa đường tròn (O));

\(\widehat {HBF} = \widehat {ABC}\,\,\left( {cmt} \right)\);

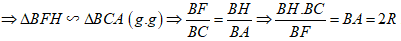
Câu 5.

Ta có: \(xy + 1 \le x,\,\,(x,y > 0) \Leftrightarrow y + \dfrac{1}{x} \le 1\)

Áp dụng BĐT Cô si, ta có:  \(y + \dfrac{1}{x} \ge 2\sqrt {y.\dfrac{1}{x}}  = 2\sqrt {\dfrac{y}{x}}  \)

\(\Rightarrow 1 \ge 2\sqrt {\dfrac{y}{x}}  \Leftrightarrow 0 < \dfrac{y}{x} \le \dfrac{1}{4}\)

\(Q = \dfrac{{x + y}}{{\sqrt {3{x^2} - xy + {y^2}} }} = \dfrac{{1 + \dfrac{y}{x}}}{{\sqrt {3 - \dfrac{y}{x} + \dfrac{{{y^2}}}{{{x^2}}}} }}\) . Đặt \(\dfrac{y}{x} = a,\,\,0 < a \le \dfrac{1}{4}\), ta có:

\(Q = \dfrac{{1 + a}}{{\sqrt {3 - a + {a^2}} }} = \sqrt {\dfrac{{{a^2} + 2a + 1}}{{{a^2} - a + 3}}} \) , \(0 < a \le \dfrac{1}{4}\)

Ta chứng minh: \(\dfrac{{{a^2} + 2a + 1}}{{{a^2} - a + 3}} \le \dfrac{5}{9}\,\,(*),\,\,\forall 0 < a \le \dfrac{1}{4}\)

\(\left( * \right) \Leftrightarrow 9({a^2} + 2a + 1) \le 5({a^2} - a + 3)\) ( do \({a^2} - a + 3 > 0,\,\,\forall a\))

\( \Leftrightarrow 4{a^2} + 23a - 6 \le 0 \)

\(\Leftrightarrow 4{a^2} - a + 24a - 6 \le 0\)

\(\Leftrightarrow a(4a - 1) + 6(4a - 1) \le 0\)

\(\Leftrightarrow (4a - 1)(a + 6) \le 0\)

Do \(0 < a \le \dfrac{1}{4}\) \( \Rightarrow 4a - 1 \le 0,\,\,a + 6 > 0 \Rightarrow (4a - 1)(a + 6) \le 0\)

\( \Rightarrow \dfrac{{{a^2} + 2a + 1}}{{{a^2} - a + 3}} \le \dfrac{5}{9}\,\,,\,\,\forall 0 < a \le \dfrac{1}{4}\)

\( \Rightarrow Q = \sqrt {\dfrac{{{a^2} + 2a + 1}}{{{a^2} - a + 3}}}  \le \sqrt {\dfrac{5}{9}}  = \dfrac{{\sqrt 5 }}{3}\),\(\forall 0 < a \le \dfrac{1}{4}\)

Vậy, \({Q_{max}} = \dfrac{{\sqrt 5 }}{3}\) khi và chỉ khi \(a = \dfrac{1}{4} \Leftrightarrow \left\{ \begin{array}{l}\dfrac{y}{x} = \dfrac{1}{4}\\y + \dfrac{1}{x} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = \dfrac{1}{2}\end{array} \right.\)