Bài 1.1, 1.2, 1.3, 1.4, 1.5 phần bài tập bổ sung trang 138,139 SBT toán 6 tập 1

Bài I.1

Chọn đáp án đúng. 

Quan sát hình bs 6. 

(A) đường thẳng \(d\) đi qua điểm \(T.\)

(B) đường thẳng \(d\) đi qua hai điểm \(M \) và \(T.\)

(C) đường thẳng \(d\) không đi qua điểm \(M\) và không đi qua điểm \(T.\)

(D) đường thẳng \(d\) đi qua điểm \(M\) và không đi qua điểm \(T.\)

Ta thấy đường thẳng \(d\) đi qua điểm \(M\) và không đi qua điểm \(T.\)

Chọn (D)

Bài I.2

Có thể vẽ được bao nhiêu đường thẳng đi qua hai trong số năm điểm (phân biệt), nhưng không có ba điểm nào thẳng hàng cho trước?

(A) 1;                          (B) 5;                         

(C) 10;                        (D) Vô số. 

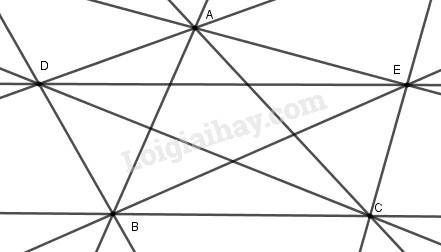
Qua \(5\) điểm phân biệt \(A,B,C,D,E\) ta vẽ được \(10\) đường thẳng: \(AB, AC,AD,AE,BC,\)\(BD,BE,CD,CE,DE.\)

Chọn (C)

Bài I.3

Với ba điểm (phân biệt) \(M, N, P\) thẳng hàng thì

(A) Điểm \(N\) luôn nằm giữa hai điểm \(M, P;\)

(B) Điểm \(M\) và điểm \(N \) luôn nằm khác phía đối với điểm \(P;\)

(C) Điểm \(N \) và điểm \(P\) luôn nằm cùng phía đối với điểm \(M;\)

(D) Hai điểm luôn nằm về một phía đối với điểm còn lại.

Trong ba điểm thẳng hàng thì hai điểm luôn nằm về một phía đối với điểm còn lại.

Đáp án (A), (B), (C) sai vì đề bài không nói rõ điểm nào nằm giữa hai điểm còn lại.

Chọn (D)  

Bài I.4

Hai tia trùng nhau nếu

(A) chúng có chung gốc và cùng nằm trên một đường thẳng;

(B) chúng có chung gốc và có một điểm chung khác với điểm gốc;

(C) chúng có hai điểm chung; 

(D) chúng có rất nhiều điểm chung. 

Hai tia trùng nhau nếu chúng có chung gốc và có một điểm chung khác với điểm gốc.

Chọn (B)

Bài I.5

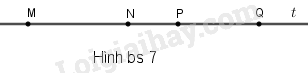
Số đoạn thẳng mà hai đầu mút của mỗi đoạn là một trong các điểm \(M, N, P, Q\) được cho trong hình bs 7 bằng:

(A) 3;                               (B) 4;

(C) 5;                               (D) 6.

Có 6 đoạn thẳng là: \(MN,MP,MQ,NP,NQ,PQ.\)

Chọn (D)

Xem lại lý thuyết về điểm và đường thẳng tại đây. 

Qua hai điểm phân biệt ta chỉ vẽ được duy nhất một đường thẳng.

Khi ba điểm cùng thuộc một đường thẳng, ta nói chúng thẳng hàng.

Khi ba điểm không cùng thuộc bất kì một đường thẳng nào, ta nói chúng không thẳng hàng.

Với \(3\) điểm \(A, C, B\) như hình vẽ sau ta có thể nói: 

- Hai điểm \(B\) và \(C\) nằm cùng phía đối với điểm \(A.\)

- Hai điểm \(A \) và \(C\) nằm cùng phía đối với điểm \(B.\)

- Hai điểm \(A\) và \(B\) nằm khác phía đối với điểm \(C.\)

- Điểm \(C\) nằm giữa \(2\) điểm \(A\) và \(B.\) 

Nhận xét: trong ba điểm thẳng hàng, có một điểm và chỉ một điểm nằm giữa hai điểm còn lại.

Hai tia trùng nhau: Tia \(Ax\) và tia \(AB\) là hai tia trùng nhau.  

Đoạn thẳng \(AB\) là hình gồm điểm \(A,\) điểm \(B\) và tất cả các điểm nằm giữa \(A\) và \(B.\)