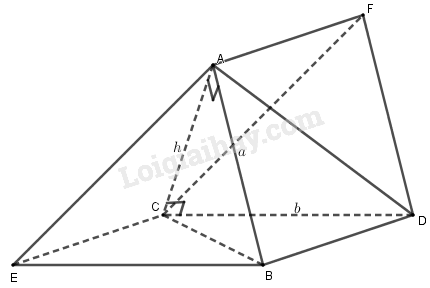
Dựng hình hình bình hành \(CDBE\) và \(ABDF\).
Khi đó, \(ABE.FDC\) là hình lăng trụ.
Ta có: \(AC \bot CD,CD//BE\) \( \Rightarrow AC \bot BE\), mà \(AC \bot AB\) nên \(AC \bot \left( {ABE} \right)\).
Lại có \(\widehat {\left( {AB,CD} \right)} = \widehat {\left( {AB,BE} \right)}\) \( = \widehat {ABE} = {60^0}\)
\( \Rightarrow {S_{ABE}} = \dfrac{1}{2}AB.BE.\sin \widehat {ABE}\)\( = \dfrac{1}{2}ab.\sin {60^0} = \dfrac{{ab\sqrt 3 }}{4}\)
\( \Rightarrow {V_{C.ABE}} = \dfrac{1}{3}{S_{ABE}}.AC\)\( = \dfrac{1}{3}.\dfrac{{ab\sqrt 3 }}{4}.h = \dfrac{{abh\sqrt 3 }}{{12}}\)
Từ đó suy ra \({V_{A.BCD}} = {V_{A.BCE}} = \dfrac{{abh\sqrt 3 }}{{12}}\).