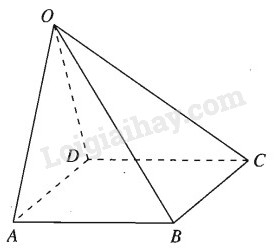
Giả sử bốn điểm \(A, B, C, D\) tạo thành một hình bình hành ta có:
\(\overrightarrow {BC} = \overrightarrow {A{\rm{D}}} \) \(\Leftrightarrow \overrightarrow {OC} - \overrightarrow {OB} = \overrightarrow {O{\rm{D}}} - \overrightarrow {OA} \) (với điểm O bất kì )
\( \Leftrightarrow \overrightarrow {OC} + \overrightarrow {OA} = \overrightarrow {O{\rm{D}}} + \overrightarrow {OB} \)
Ngược lại, giả sử ta có hệ thức:
\(\overrightarrow {OC} + \overrightarrow {OA} = \overrightarrow {O{\rm{D}}} + \overrightarrow {OB} \)
\( \Leftrightarrow \overrightarrow {OC} - \overrightarrow {OB} = \overrightarrow {O{\rm{D}}} - \overrightarrow {OA} \)
\( \Leftrightarrow \overrightarrow {BC} = \overrightarrow {A{\rm{D}}} \)
Vì \(A, B, C, D\) không thẳng hàng nên tứ giác \(ABCD\) là hình bình hành.