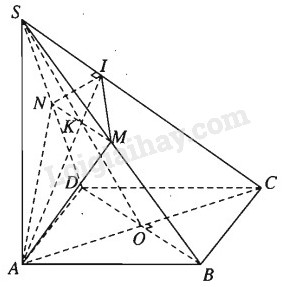
a) Gọi I là giao điểm của mặt phẳng \(\left( \alpha \right)\) với cạnh SC. Ta có \(\left( \alpha \right) \bot SC,AI \subset \left( \alpha \right) \Rightarrow SC \bot AI\). Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và \(AI \subset \left( \alpha \right)\), nên K là giao điểm của SO với \(\left( \alpha \right)\).
b) Ta có
\(\left. \matrix{
B{\rm{D}} \bot AC \hfill \cr
B{\rm{D}} \bot SA \hfill \cr} \right\} \Rightarrow B{\rm{D}} \bot \left( {SAC} \right)\)
\( \Rightarrow B{\rm{D}} \bot SC\)
Mặt khác \(B{\rm{D}} \subset \left( {SB{\rm{D}}} \right)\) nên \(\left( {SB{\rm{D}}} \right) \bot \left( {SAC} \right)\).
Vì \(B{\rm{D}} \bot SC\) và \(\left( \alpha \right) \bot SC\) nhưng BD không chứa trong \(\left( \alpha \right)\) nên \(B{\rm{D}}\parallel \left( \alpha \right)\)
Ta có \(K = SO \cap \left( \alpha \right)\) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của \(\left( \alpha \right)\) và (SBD).
Mặt phẳng (SBD) chứa \(B{\rm{D}}\parallel \left( \alpha \right)\) nên cắt theo giao tuyến \(d\parallel B{\rm{D}}\). Giao tuyến này đi qua K là điểm chung của \(\left( \alpha \right)\) và (SBD).
Gọi M và N lần lượt là giao điểm của d với SB và SD.
Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.