Tần số \(f = \dfrac{\omega }{{2\pi }} = \dfrac{{100\pi }}{{2\pi }} = 50Hz\)
Bước sóng: \(\lambda = \dfrac{v}{f} = \dfrac{{0,8}}{{50}} = 0,016m = 1,6cm\)
Xét: \( - {S_1}{S_2} < k\lambda < {S_1}{S_2}\\ \Leftrightarrow - 12 < k.1,6 < 12 \\\Leftrightarrow - 7,5 < k < 7,5\)
\( \Rightarrow k = - 7;.....;7\)
Có \(15\) giá trị của \(k\)
Quỹ tích các điểm dao động với biên độ cực đại là đường hypebol
Nếu coi đường trung trực của \({S_1}{S_2}\) như một hypebol đặc biệt thì số đường hypebol là \(15\)
Chú ý: Tại nguồn không thể có cực đại
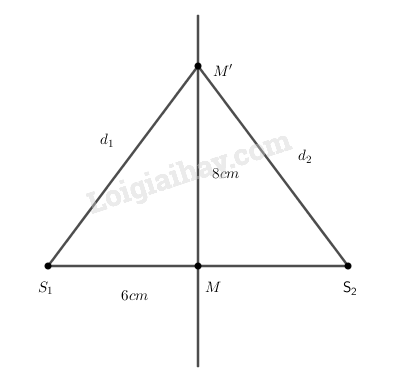
b) \(M\) cách \({S_1}{S_2}\) đoạn \({d_1} = {d_2} = 8cm\)
\(\begin{array}{l}u = 2A\cos \dfrac{{\pi ({d_2} - {d_1})}}{\lambda }cos(2\pi ft - \dfrac{{\pi ({d_2} + {d_1})}}{\lambda })\\ = 2A\cos \dfrac{{\pi .(8 - 8)}}{{1,6}}cos(2\pi .50t - \dfrac{{\pi .(8 + 8)}}{{1,6}})\\ = 2Acos(100\pi t - 10\pi ) \\= 2Acos(100\pi t)(cm)\end{array}\)
\(M'\) cách \({S_1}{S_2}\) đoạn \(8cm \Rightarrow {d_1} = {d_2} = \sqrt {{8^2} + {6^2}} = 10cm\)
\(\begin{array}{l}u = 2A\cos \dfrac{{\pi ({d_2} - {d_1})}}{\lambda }cos(2\pi ft - \dfrac{{\pi ({d_2} + {d_1})}}{\lambda }) = 2A\cos \dfrac{{\pi .(10 - 10)}}{{1,6}}cos(2\pi .50t - \dfrac{{\pi .(10 + 10)}}{{1,6}})\\ = 2Acos(100\pi t - \dfrac{{25\pi }}{2}) \\= 2Acos(100\pi t - \dfrac{\pi }{2})(cm)\end{array}\)