Câu 5 trang 34 SGK Hình học 11 Nâng cao

Bài 5. Cho tam giác ABC nội tiếp trong đường tròn (O) và một điểm M thay đổi trên (O). Gọi M₁ là điểm đối xứng với M qua A, M₂ là điểm đối xứng với M₁ qua B, M₃ là điểm đối xứng với M₂ qua C

a. Chứng tỏ rằng phép biến hình F biến điểm M thành M₃ là một phép đối xứng tâm

b. Tìm quỹ tích điểm M₃

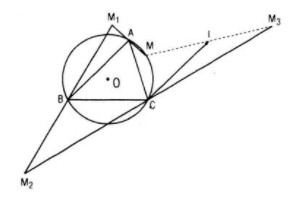
a. Gọi I là trung điểm của MM₃, ta chứng minh I là điểm cố định

Thật vậy, ta có:

\(\eqalign{
& \overrightarrow {CI} = {1 \over 2}\left( {\overrightarrow {CM} + \overrightarrow {C{M_3}} } \right) \cr
& \,\,\,\,\,\,\, = {1 \over 2}\left( {\overrightarrow {CM} + \overrightarrow {{M_2}C} } \right) \cr
& \,\,\,\,\,\,\, = {1 \over 2}\overrightarrow {{M_2}M} = \overrightarrow {BA} \cr} \)

Như vậy điểm I cố định, do đó phép biến hình F biến M thành M₃ là phép đối xứng qua điểm I

b. Quỹ tích điểm M₃ là đường tròn (O’), ảnh của đường tròn (O) qua phép đối xứng tâm với tâm I