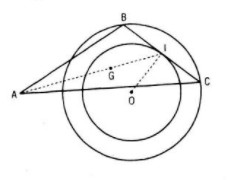
Gọi I là trung điểm của BC
Ta có
\(\eqalign{
& \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \cr
& \Leftrightarrow \overrightarrow {GA} + 2\overrightarrow {GI} = \overrightarrow 0 \cr
& \Leftrightarrow \overrightarrow {AG} = {2 \over 3}\overrightarrow {AI} \cr} \)
Tức là phép vị tự V tâm A tỉ số \({2 \over 3}\) biến điểm I thành điểm G
Trong tam giác vuông OIB ta có:
\(OI = \sqrt {O{B^2} - I{B^2}} = \sqrt {{R^2} - {{\left( {{m \over 2}} \right)}^2}} = R'\) (không đổi)
Nên quỹ tích I là đường tròn (O ; R’) hoặc là điểm O (nếu m = 2R)
Do đó quỹ tích G là ảnh của quỹ tích I qua phép vị tự V