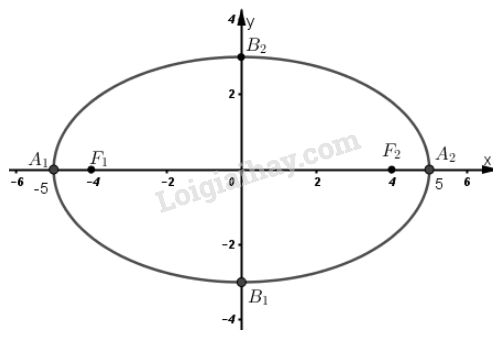
a) Ta có: \(a^2= 25 \Rightarrow a = 5\) độ dài trục lớn \(2a = 10\)
\( b^2= 9 \Rightarrow b = 3\) độ dài trục nhỏ \(2a = 6\)
\(c^2= a^2– b^2= 25 - 9 = 16 \Rightarrow c = 4\)
Vậy hai tiêu điểm là : \(F_1(-4 ; 0)\) và \(F_2(4 ; 0)\)
Tọa độ các đỉnh \(A_1(-5; 0), A_2(5; 0), B_1(0; -3), B_2(0; 3)\).
b) \(4x^2+ 9y^2= 1\Leftrightarrow \frac{x^{2}}{\frac{1}{4}} + \frac{y^{2}}{\frac{1}{9}} = 1\)
\(a^2 =\frac{1}{4}\Rightarrow a = \frac{1}{2}\) \(\Rightarrow\) độ dài trục lớn \(2a = 1\)
\(b^2= \frac{1}{9}\Rightarrow b = \frac{1}{3}\) \(\Rightarrow\) độ dài trục nhỏ \(2b = \frac{2}{3}\)
\(c^2= a^2– b^2= \frac{1}{}4- \frac{1}{9} = \frac{5}{36}\) \(\Rightarrow c = \frac{\sqrt{5}}{6}\)
\(F_1(-\frac{\sqrt{5}}{6} ; 0)\) và \(F_2(\frac{\sqrt{5}}{6} ; 0)\)
\(A_1(-\frac{1}{2}; 0), A_2(\frac{1}{2}; 0)\), \(B_1(0; -\frac{1}{3} ), B_2(0; \frac{1}{3} )\).
c) Chia \(2\) vế của phương trình cho \(36\) ta được :
\(\frac{x^{2}}{9}+ \frac{y^{2}}{4}= 1\)
Từ đây suy ra: \(2a = 6, 2b = 4, c = \sqrt5\)
Suy ra \(F_1(-\sqrt5 ; 0)\) và \(F_2(\sqrt5 ; 0)\)
\(A_1(-3; 0), A_2(3; 0), B_1(0; -2), B_2(0; 2)\).