Ôn tập chương III - Phương pháp tọa độ trong mặt phẳng

Cho hình chữ nhật \(ABCD\). Biết các đỉnh \(A(5; 1), C(0; 6)\) và phương trình \(CD: x + 2y – 12 = 0.\)

Tìm phương trình các đường thẳng chứa các cạnh còn lại.

Cho \(A(1; 2), \, \, B(-3; 1)\) và \(C(4; -2)\). Tìm tập hợp điểm \(M\)  sao cho \(M{A^2} + M{B^2} = M{C^2}\)

Tìm tập hợp các điểm cách đều hai đường thẳng: \({\Delta _1} : 5x + 3y – 3 = 0\) và  \({\Delta _2}: 5x + 3y + 7 = 0.\)

Cho đường thẳng \(Δ: x – y + 2\) và hai điểm \(O(0; 0); \, A(2; 0).\)

a) Tìm điểm đối xứng của \(O\) qua \(Δ\)

b) Tìm điểm \(M\) trên \(Δ\) sao cho độ dài đường gấp khúc \(OMA\) ngắn nhất.

Cho ba điểm \(A(4; 3), B(2; 7), C(-3; -8)\)

a) Tìm tọa độ điểm \(G\) , trực tâm \(H\) của tam giác \(ABC\).

b) Tìm \(T\) là trực tâm của đường tròn ngoại tiếp tam giác \(ABC\). Chứng minh \(T, G, H\) thẳng hàng.

c) Viết phương trình đường tròn ngoại tiếp tam giác \(ABC\).

Lập phương trình hai đường phân giác của các góc tạo bởi đường thẳng \(3x – 4y + 12 = 0\) và \(12x+5y-7 = 0.\)

Cho đường tròn \((C)\) có tâm \(I(1; 2)\) và bán kính bằng \(3\). Chứng minh rằng tập hợp các điểm \(M\) từ đó ta sẽ được hai tiếp tuyến với \((C)\) tạo với nhau một góc \(60^0\) là một đường tròn. Hãy viết phương trình đường tròn đó.

Tìm góc giữa hai đường thẳng \(\Delta_1\) và \(\Delta_2\) trong các trường hợp sau:

a) \(\Delta_1\): \(2x + y – 4 = 0\) ; \(\Delta_2\): \(5x – 2y + 3 = 0.\)

b) \(\Delta_1\): \(y = -2x + 4\)  ;   \({\Delta _2}:y = {1 \over 2}x + {3 \over 2}.\)  

Cho elip \((E) = {{{x^2}} \over {16}} + {{{y^2}} \over 9} = 1\) . Tìm tọa độ các đỉnh, các tiêu điểm và vẽ elip đó.

Ta biết rằng Mặt trăng chuyển động quanh Trái Đất theo một quỹ đạo là một elip mà Trái Đất là một tiêu điểm. Elip đó có chiều dài trục lớn và trục nhỏ lần lượt là \(769 266 km\) và \(768 106 km\). Tính khoảng cách ngắn nhất và khoảng cách dài nhất từ Trái Đất đến Mặt Trăng, biết rằng các khoảng cách đó đạt được khi Trái Đất và Mặt Trăng nằm trên trục lớn của Elip.

Cho tam giác \(ABC\) có tọa độ các đỉnh \(A(1; 2), B(3; 1)\) và \(C(5; 4)\). Phương trình nào sau đây là phương trình đường cao của tam giác vẽ từ \(A\)?

A. \(2x + 3y – 8 = 0\)    

B. \(3x – 2y – 5 = 0\)

C. \(5x – 6y + 7 = 0\)    

D. \(3x – 2y + 5 = 0\)

Cho tam giác \(ABC\) với \(A(-1; 1), B(4; 7)\) và \(C(3; 2)\). Phương trình tham số của trung tuyến CM là:

A. \(\left\{ \matrix{x = 3 + t \hfill \cr y = - 2 + 4t \hfill \cr} \right.\)

B.  \(\left\{ \matrix{x = 3 + t \hfill \cr y = - 2 - 4t \hfill \cr} \right.\)

C. \(\left\{ \matrix{x = 3 - t \hfill \cr y = 4 + 2t \hfill \cr} \right.\)

D. \(\left\{ \matrix{x = 3 + 3t \hfill \cr y = - 2 + 4t \hfill \cr} \right.\)

Cho phương trình tham số của đường thẳng \(d\):  \(\left\{ \matrix{x = 5 + t \hfill \cr y = - 9 - 2t \hfill \cr} \right.\)

Trong các phương trình sau, phương trình nào là tổng quát của (d)?

A. \(2x + y – 1 = 0\)

B. \(2x + 3y + 1 = 0\)

C. \(x + 2y + 2 = 0\)              

D. \(x + 2y – 2 = 0\)

Đường thẳng đi qua điểm \(M(1; 0)\) và song song với đường thẳng \(d: 4x + 2y + 1 = 0\) có phương trình tổng quát là:

A. \(4x + 2y + 3 = 0\) 

B. \(2x + y + 4 = 0\)

C. \(2x + y – 2 = 0\)  

D. \(x – 2y + 3 = 0\)

Cho đường thẳng \(d\) có phương trình tổng quát: \(3x + 5y + 2006 = 0\).

Tìm mệnh đề sai trong các mệnh đề sau:

A. \(d\) có vecto pháp tuyến \(\overrightarrow n  = (3;5)\)

B. \(d\) có vecto chỉ phương \(\overrightarrow a  = (5; - 3)\)

C. \(d\) có hệ số góc \(k = {5 \over 3}\)

D. \(d\) song song với đường thẳng \(3x + 5y = 0\)

Bán kính của đường tròn tâm \(I(0; 2)\) và tiếp xúc với đường thẳng \(Δ: 3x – 4y – 23 = 0\) là:

A. \(15\)                                  B. \(5\)     

C. \({3 \over 5}\)                                   D. \(3\)

Cho hai đường thẳng:

           \(d_1: 2x + y  + 4 – m = 0\)

           \(d_2: (m + 3)x + y – 2m – 1 = 0\)

Đường thẳng \(d_1//d_2\) khi:

A. \(m = 1\)                              B. \(m = -1\)    

C. \(m = 2\)                              D. \(m = 3\)

Cho \(d_1: x + 2y + 4 = 0\) và \(d_2: 2x – y + 6 = 0\). Số đo của góc giữa hai đường thẳng \(d_1\) và \(d_2\) là:

A. \(30^0\)                              B. \(60^0\) 

C. \(45^0\)                              D. \(90^0\)

Cho hai đường thẳng \(\Delta_1: x + y + 5 = 0\) và  \(\Delta_2: y  = -10.\) Góc giữa \(\Delta_1\) và \(\Delta_2\) là:

A. \(45^0\)                                 B. \(30^0\)  

C. \(88^057’52’’\)                      D. \(1^013’8’’\)

Khoảng cách từ điểm \(M(0; 3)\) đến đường thẳng  \(Δ: x\cos α + y \sin α + 3(2 - \sin α) = 0\) là:

A. \(\sqrt6\)                           B. \(6\)  

C. \(3\sin α\)                      D. \({3 \over {\sin \alpha  + \cos \alpha }}\)

Phương trình nào sau đây là phương trình đường tròn?

A. \(x^2+ 2y^2– 4x – 8y + 1 = 0\)

B. \(4x^2+ y^2– 10x – 6y  -2  = 0\)

C. \(x^2+ y^2– 2x – 8y + 20 = 0\)

D. \(x^2+ y^2– 4x + 6y - 12 = 0\)

Cho đường tròn (C): \(x^2+ y^2+ 2x + 4y – 20 = 0\)

Tìm mệnh đề sai trong các mệnh đề sau:

A. (C) có tâm \(I(1; 2)\)

B. (C) có bán kính \(R = 5\)

C. (C) đi qua điểm \(M(2; 2)\)

D. (C) không đi qua \(A(1; 1)\)

Phương trình tiếp tuyến tại điểm \(M(3; 4)\) với đường tròn \((C): x^2+y^2– 2x – 4y – 3 = 0.\)

A.\( x + y – 7 = 0\)

B.\( x + y + 7 = 0\)

C.\( x – y – 7 = 0\)     

D. \(x + y – 3 = 0\)

Cho đường tròn (C) : \(x^2+ y^2– 4x – 2y = 0\) và đường thẳng \(Δ: x + 2y + 1 = 0\)

Trong các mệnh đề sau, tìm mệnh đề đúng:

A. \(Δ\) đi qua tâm \((C)\)                            

B. \(Δ\) cắt \((C)\) tại hai điểm

C. \(Δ\) tiếp xúc \((C)\)                                

D. \(Δ\) không có điểm chung với \((C)\)

Đường tròn \((C): x^2+ y^2– x + y – 1 = 0\) có tâm \(I\) và bán kính \(R\) là:

A. \(I(-1; \,  1); R = 1\)           

B. \(I({1 \over 2}; - {1 \over 2});R = {{\sqrt 6 } \over 2}\)

C. \(I( - {1 \over 2};{1 \over 2});R = {{\sqrt 6 } \over 2}\)                  

D. \(I(1; -1); R = \sqrt6\)

Với giá trị nào của m thì phương trình sau đây là phương trình của đường tròn: \(x^2+ y^2– 2(m+2)x + 4my + 19m – 6 \)\(= 0\)

A.  \(1 < m < 2\)                               

B. \(-2 ≤ m ≤ 1\)

C. \(m < 1\)  hoặc \(m > 2\)                

D. \(m < -2\)  hoặc \(m > 1\)

Đường thẳng \(Δ: 4x + 3y + m = 0\) tiếp xúc với đường tròn \((C): x^2+ y^2=1\) khi:

A. \(m = 3\)                        B. \(m = 5\)  

C. \(m = 1\)                        D. \(m = 0\)

Cho hai điểm \(A(1; 1)\) và \(B(7; 5)\). Phương trình đường tròn đường kính \(AB\) là:

A. \(x^2+ y^2 + 8x + 6y + 12 = 0\) 

B. \(x^2+ y^2- 8x - 6y + 12 = 0\) 

C. \(x^2+ y^2- 8x - 6y - 12 = 0\)   

D. \(x^2+ y^2+ 8x + 6y - 12 = 0\)  

Đường tròn đi qua ba điểm \(A(0; 2); B(-2; 0)\) và \(C(2; 0)\) có phương trình là:

A. \(x^2+ y^2 =8\)

B. \(x^2+ y^2+ 2x + 4 = 0\)

C. \(x^2+ y^2- 2x - 8 = 0\)                    

D. \(x^2+ y^2- 4 = 0\)

Cho điểm \(M(0; 4)\) và đường tròn \((C)\) có phương trình: \(x^2+ y^2- 8x – 6y + 21 = 0\)

Trong các phát biểu sau, tìm phát biểu đúng:

A. \(M\) nằm ngoài \((C)\)    

B. \(M\) nằm trên \((C)\)

C. \(M\) nằm trong \((C)\)

D. \(M\) trùng với tâm của \((C)\)

Cho elip \((E)\): \({{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\) và cho các mệnh đề:

(I) \((E)\) có tiêu điểm \(F_1( -4; 0)\) và \(F_2( 4; 0)\)

(II) \((E)\) có tỉ số \({c \over a} = {4 \over 5}\)

(III) \((E)\) có đỉnh \(A_1(-5; 0)\)

(IV) \((E)\) có độ dài trục nhỏ bằng \(3\).

Trong các mệnh đề sau, tìm mệnh đề sai:

A. (I) và (II)   

B. (II) và (III)

C. (I) và (III)    

D. (IV) và (I)

Phương trình chính tắc của elip có hai đỉnh là \((-3; 0), (3; 0)\) và hai tiêu điểm là \((-1; 0), (1; 0)\) là:

A. \({{{x^2}} \over 9} + {{{y^2}} \over 1} = 1\)  

B. \({{{x^2}} \over 8} + {{{y^2}} \over 9} = 1\)

C. \({{{x^2}} \over 9} + {{{y^2}} \over 8} = 1\)     

D. \({{{x^2}} \over 1} + {{{y^2}} \over 9} = 1\)

Cho elip \((E): x^2+ 4y^2= 1\) và cho các mệnh đề:

(I): \((E)\) có trục lớn bằng \(1\)

(II) \((E)\) có trục nhỏ bằng \(4\)

(III) \((E)\) có tiêu điểm \({F_1}(0; \, {{\sqrt 3 } \over 2})\)

(IV) \((E)\) có tiêu cự bằng \(\sqrt3\).

Trong các mệnh đề sau, tìm mệnh đề đúng:

A. (I)                                      B. (II) và (IV)

C. (I)  và (III)                          D. (IV)

Dây cung của elip (E): \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1  (0 < b < a)\) vuông góc với trục lớn tại tiêu điểm có độ dài là:

A. \({{2{c^2}} \over a}\)                      B. \({{2{b^2}} \over a}\)                            

C. \({{2{a^2}} \over c}\)                      D. \({{{a^2}} \over c}\)

Một elip có trục lớn là \(26\), tỉ số \({c \over a} = {{12} \over {13}}\) . Trục nhỏ của elip bằng bao nhiêu?

A. \(5\)                         B. \(10\)                      

C. \(12\)                       D. \(14\)

Cho elip \((E): 4x^2+ 9y^2= 36\). Trong các mệnh đề sau, tìm mệnh đề sai:

A. \((E)\) có trục lớn bằng \(6\)

B. \((E)\) có trục nhỏ bằng \(4\)

C. \((E)\) có tiêu cự bằng  \(\sqrt5\) 

D. \((E)\) có tỉ số \({c \over a} = {{\sqrt 5 } \over 3}\)

Cho đường tròn \((C)\) tâm \(F_1\) bán kính \(2a\) và một điểm \(F_2\) ở bên trong của \((C)\). Tập hợp điểm \(M\) của các đường tròn \((C’)\) thay đổi nhưng luôn đi qua \(F_2\) và tiếp xúc với \((C)\) (xem hình) là đường nào sau đây?

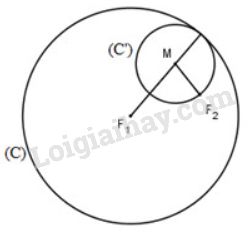
A. Đường thẳng                             

B. Đường tròn

C. Elip                                           

D. Parabol

Khi \(t\) thay đổi,  điểm \(M(5cost; 4sint)\) di động trên đường tròn nào sau đây:

A. Elip                            B. Đường thẳng

C. Parabol                      D. Đường tròn

Cho elip \((E)\): \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1(0 < b < a)\). Gọi \(F_1,F_2\) là hai tiêu điểm và cho điểm \(M(0; -b)\)

Giá trị nào sau đây bằng giá trị của biểu thức : \(MF_1– MF_2– OM^2\)

A. \(c^2\)                                      B. \(2a^2\)   

C. \(2b^2\)                                    D. \(a^2– b^2\)

Cho elip \((E) {{{x^2}} \over {16}} + {{{y^2}} \over 9} = 1\) :  và đường thẳng \(Δ: y + 3 = 0\)

Tích các khoảng cách từ hai tiêu điểm của \((E)\) đến đường thẳng \(Δ\) bằng các giá trị nào sau đây:

A. \(16\)                        B. \(9\)                          

C. \(81\)                        D. \(7\)