Bài 3. Phương trình đường Elip

Quan sát mặt nước trong cốc nước cầm nghiêng (h.3.18a). Hãy cho biết đường được đánh dấu bởi mũ tên có phải là đường tròn hay không ?

Hãy cho biết bóng của một đường tròn trên một mặt phẳng (h.3.18b) có phải là một đường tròn hay không ?

Trong phương trình (1) hãy giải thích vì sao ta luôn đặt được b² = a² - c².

Hãy xác định tọa độ các tiêu điểm và hình vẽ elip trong ví dụ trên.

Xác đinh độ dài các trục, tọa độ tiêu điểm, tọa độ các đỉnh và vẽ các elip có phương trình sau:

a) \(\frac{x^{2}}{25} + \frac{y^{2}}{9}= 1.\)

b) \(4x^2+ 9y^2= 1.\)

c) \(4x^2+ 9y^2= 36.\)

Lập phương trình chính tắc của elip, biết:

a)  Trục lớn và trục nhỏ lần lươt  là \(8\) và \(6.\)

b) Trục lớn bằng \(10\) và tiêu cự bằng \(6.\)

Lập phương trình chính tắc của elip trong các trường hợp sau:

a) Elip đi qua các điểm \(M(0; 3)\) và \(N( 3; \frac{-12}{5}).\)

b) Một tiêu điểm là \(F_1( -\sqrt3; 0)\) và điểm \(M(1; \frac{\sqrt{3}}{2})\) nằm trên elip.

Để cắt một bảng hiệu quảng cáo hình elip có các trục lớn là \(80cm\) và trục nhỏ là \(40 cm\) từ một tấm ván ép hình chữ nhật có kích thước \(80cm \times 40cm\), người ta vẽ một hình elip lên tấm ván như hình 3.19. Hỏi phải ghim hai cái đinh cách các mép tấm ván ép bao nhiêu và lấy vòng dây có độ dài là bao nhiêu?

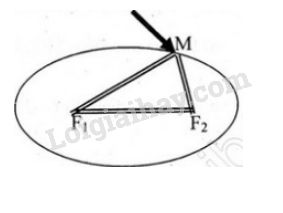
Cho hai đường tròn \({C_1}({F_1};{R_1})\)  và \({C_2}({F_2};{R_2})\). \(C_1\) nằm trong \(C_2\) và \(F_1≠  F_2\). Đường tròn \((C)\)  thay đổi luôn tiếp xúc ngoài với \(C_1\) và tiếp xúc trong với \(C_2\).Hãy chứng tỏ rằng tâm \(M\) của đường tròn \((C)\) di động trên một elip.