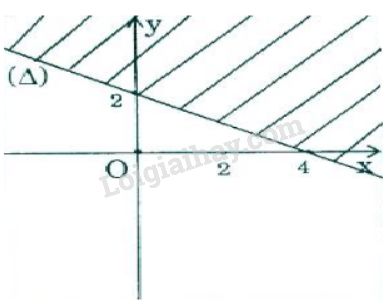
a) \(- x + 2 + 2(y - 2) < 2(1 - x) \)
\(\Leftrightarrow - x + 2 + 2y - 4 < 2 - 2x \)
\(\Leftrightarrow x - 4 + 2y < 0 \Leftrightarrow y < -\frac{x}{2}+2.\)
Tập nghiệm của bất phương trình là:
\(T = \left\{ {(x;y)|x \in\mathbb R;y < - {x \over 2} + 2} \right\}\)
Để biểu diễn tập nghiệm \(T\) trên mặt phẳng tọa độ, ta thực hiện:
+ Vẽ đường thẳng \((d): y= -\frac{x}{2}+2.\)
+ Lấy điểm gốc tọa độ \(O(0; 0)\) \(\notin (d)\).
Ta thấy: \(0 < -\frac{1}{2} - 0 + 2\). Chứng tỏ \((0; 0)\) là một nghiệm của bất phương trình. Vậy nửa mặt phẳng bờ là đường thẳng \((d)\) (không kể bờ) chứa gốc \(O(0; 0)\) là tập hợp các điểm biểu diễn tập nghiệm của bất phương trình đã cho (nửa mặt phẳng không bị gạch sọc)
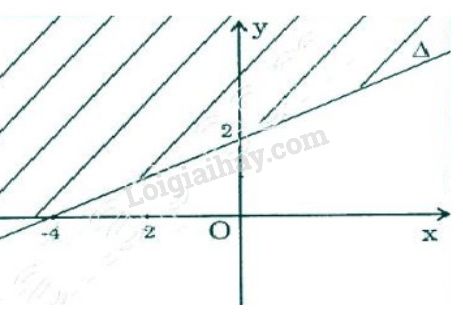
b) \(3(x - 1) + 4(y - 2) < 5x - 3\)
\(\eqalign{
& \Leftrightarrow 3x - 3 + 4y - 8 - 5x + 3 < 0 \cr
& \Leftrightarrow - 2x + 4y - 8 < 0 \cr
& \Leftrightarrow x - 2y + 4 > 0 \cr} \)
Tập nghiệm của bất phương trình là:
\(T = \left\{ {(x;y)|x,y \in\mathbb R;x - 2y > -4} \right\}\)
+) Vẽ đường thẳng \((\Delta): x-2y+4=0\)
+) Lấy điểm \(O(0;0)\) \(\notin (\Delta)\)
Ta thấy \(0-2.0+4=4>0\). Chứng tở \((0;0)\) là một nghiệm của bất phương trình. Vậy nửa mặt phẳng bờ là đường thẳng \((\Delta)\) (không kể bờ) chứa gốc \(O(0; 0)\) là tập hợp các điểm biểu diễn tập nghiệm của bất phương trình đã cho (nửa mặt phẳng không bị gạch sọc)