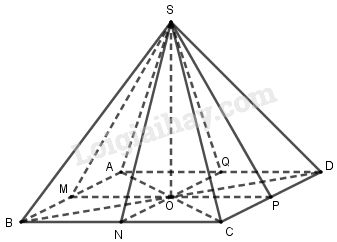
Gọi \(O = AC \cap BD\), các điểm \(M,N,P,Q\) lần lượt là trung điểm của mỗi đoạn thẳng \(AB,BC,CD,DA\).
Khi đó các tam giác \(AOM,BOM,BON,CON,\) \(COP,DOP,DOQ,AOQ\) bằng nhau.
Ta chứng minh các hình chóp \(S.AOM,S.BOM,S.BON,S.CON,\) \(S.COP,S.DOP,S.DOQ,S.AOQ\) bằng nhau.
Xét hai hình chóp \(S.AOM\) và \(S.BOM\) có \(SA = SB,AO = BO,AM = BM,\) \(SO\) chung và \(SM\) chung, \(OM\) chung.
Do đó hai tứ diện có các cạnh tương ứng bằng nhau thì bằng nhau.
Tương tự ta có \(8\) hình chóp bằng nhau.