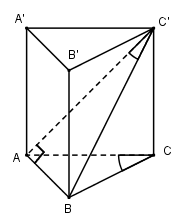
a) Ta có: \(BA \bot AC\) và \(BA \bot AA'\) nên \(BA \bot \left( {ACC'A'} \right)\)
Vậy \(AC’\) là hình chiếu của \(BC’\) trên mp \((ACC’A’)\) nên \(\widehat {AC'B} = {30^0}\)
Trong tam giác vuông \(BAC’\), ta có: \(\cot {30^0} = {{AC'} \over {AB}} \Rightarrow AC' = AB.cot{30^0} = AC.\tan {60^0}.\cot {30^0} = b\sqrt 3 .\sqrt 3 = 3b\)
b) Trong tam giác vuông \(ACC’\), ta có: \(CC{'^2} = AC{'^2} - A{C^2} = 9{b^2} - {b^2} = 8{b^2} \Rightarrow CC' = 2\sqrt 2 b\)
Diện tích là: \({S_{ABC}} = {1 \over 2}AB.AC = {1 \over 2}b\sqrt 3 .b = {{{b^2}\sqrt 3 } \over 2}\)
Thể tích khối lăng trụ \(V = S.h = {{{b^2}\sqrt 3 } \over 2}.2\sqrt 2 b = {b^3}\sqrt 6 \)