Bài 2.43 trang 65 SBT hình học 12

Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 2a\) và \(\widehat B = {30^0}\). Quay tam giác vuông này quanh trục \(AB\), ta được một hình nón đỉnh \(B\). Gọi \({S_1}\) là diện tích toàn phân của hình nón đó và \({S_2}\) là diện tích mặt cầu có đường kính \(AB\). Khi đó, tỉ số \(\dfrac{{{S_1}}}{{{S_2}}}\) là:

A. \(1\)                          B. \(\dfrac{1}{2}\)

C. \(\dfrac{2}{3}\)                      D. \(\dfrac{3}{2}\)

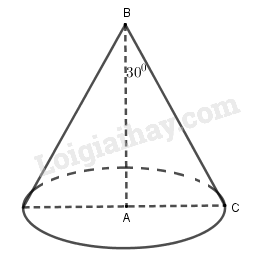
Tam giác \(ABC\) vuông tại \(A\) có \(AC = BC\sin {30^0} = a\); \(AB = BC\cos {30^0} = a\sqrt 3 \).

Diện tích toàn phần hình nón là:

\({S_1} = {S_{xq}} + {S_d}\) \( = \pi rl + \pi {r^2}\) \( = \pi a.2a + \pi {a^2}\) \( = 2\pi {a^2} + \pi {a^2} = 3\pi {a^2}\)

Diện tích mặt cầu đường kính \(AB\) là:

\({S_2} = \pi A{B^2} = \pi {\left( {a\sqrt 3 } \right)^2} = 3\pi {a^2}\).

Vậy \(\dfrac{{{S_1}}}{{{S_2}}} = 1\).

Chọn A.