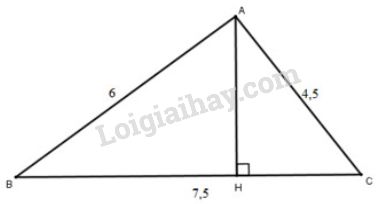
a) Ta có: \({6^2} + 4,{5^2} = 36 + 20,25 = 56,25 = 7,{5^2}.\)
\(\Rightarrow ∆ABC\) có \(AB^2+AC^2=BC^2(=56,25)\) nên vuông tại \(A\) (định lý Pi-ta-go đảo).
\(\eqalign{&Ta \, \, có: tan B = {{AC} \over {AB}} = {{4,5} \over 6} = 0,75 \Rightarrow \widehat B \approx {37^0} \cr & \Rightarrow \widehat C = {90^0} - \widehat B \approx {53^0}. \cr} \)
Xét \(∆ABC\) vuông tại \(A, \, \, AH\) là đường cao nên:
\(AH.BC = AB.AC\)
\( \displaystyle \Rightarrow AH = {{AB.AC} \over {BC}} = {{4,5.6} \over {7,5}} = 3,6(cm).\)
b)
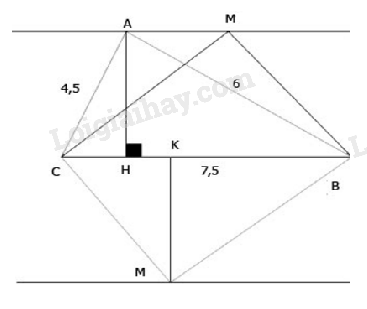
Kẻ \(MK \bot BC\) tại \(K.\)
Ta có: \(S_{ABC}=\dfrac{1}{2}AH.BC\)
\(S_{MBC}=\dfrac{1}{2}MK.BC\)
\(\Rightarrow S_{ABC}=S_{MBC} \Leftrightarrow MK= AH.\)
Do đó \(M\) nằm trên hai đường thẳng song song cách \(BC\) một khoảng bằng \(3,6 cm\) (hình vẽ).