Ôn tập chương I – Hệ thức lượng giác trong tam giác vuông

Chọn kết quả đúng trong các kết quả dưới đây:

a) Trong hình 41, sinα bằng

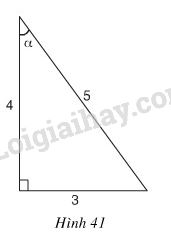
(A) \( \displaystyle{5 \over 3}\)                     (B) \( \displaystyle{5 \over 4}\)                    (C) \( \displaystyle{3 \over 5}\)                    (D) \( \displaystyle{3 \over 5}\)

b) Trong hình 42, sin Q bằng

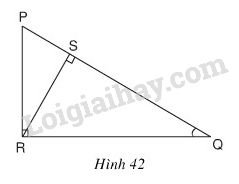
(A) \( \displaystyle{{P{\rm{R}}} \over {R{\rm{S}}}}\)              (B) \( \displaystyle{{P{\rm{R}}} \over {QR}}\)               (C) \( \displaystyle{{P{\rm{S}}} \over {S{\rm{R}}}}\)                (D) \( \displaystyle{{S{\rm{R}}} \over {Q{\rm{R}}}}\) 

c) Trong hình 43, cos 30° bằng

(A) \( \displaystyle{{2{\rm{a}}} \over {\sqrt 3 }}\)                (B) \( \displaystyle{a \over {\sqrt 3 }}\)               (C) \( \displaystyle{{\sqrt 3 } \over 2}\)               (D) \( \displaystyle2\sqrt 3 {a^2}\)   

Chọn kết quả đúng trong các kết quả dưới đây:

a) Trong hình 44, hệ thức nào trong các hệ thức sau là đúng? 

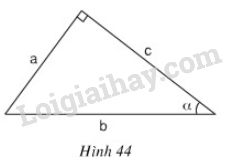
(A) \( \displaystyle \sin \alpha  = {b \over c}\)                   (B) \( \displaystyle {\mathop{\rm cotg}\nolimits} \alpha  = {b \over c}\) 

(C) \( \displaystyle tg \alpha  = {a \over c}\)                      (D) \( \displaystyle {\mathop{\rm cotg}\nolimits} \alpha  = {a \over c}\)

b) Trong hình 45, hệ thức nào trong các hệ thức sau không đúng?

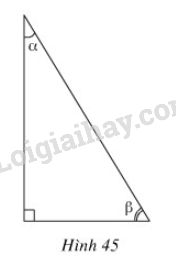
(A) \( \displaystyle \sin^2 α + cos^2 α = 1\);

(B) \( \displaystyle \sin α = cos β\);

(C) \( \displaystyle \cos β = sin(90°- α)\);

(D) \( \displaystyle tg \alpha  = {{\sin \alpha } \over {\cos \alpha }}\) 

Tỉ số giữa hai cạnh góc vuông của một hình tam giác vuông bằng 19 : 28. Tìm các góc của nó.

\(\displaystyle tg\alpha  = {{19} \over {28}} \approx 0,6786 \Rightarrow \alpha  \approx {34^0}10'\)

Vậy các góc nhọn của tam giác vuông đó có độ lớn là:

\(α ≈ 34°10’;\, \,  β ≈ 90° - 34°10’ = 55°50’.\) 

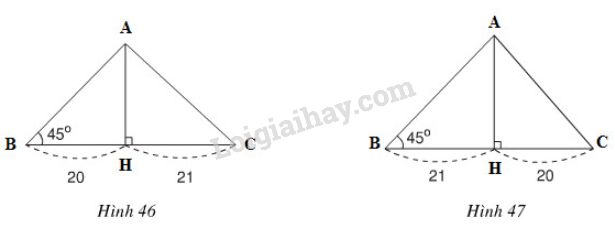
Cho tam giác có một góc bằng 45°. Đường cao chia một cạnh kề với góc đó thành các phần 20cm và 21cm. Tính cạnh lớn trong hai cạnh còn lại (lưu ý có hai trường hợp hình 46 và hình 47)

Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.

a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.

b) Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nắm trên đường nào?

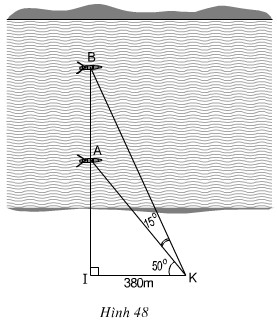
Hai chiếc thuyền A và B ở vị trí được minh họa như trong hình 48. Tính khoảng cách giữa chúng (làm tròn đến mét)

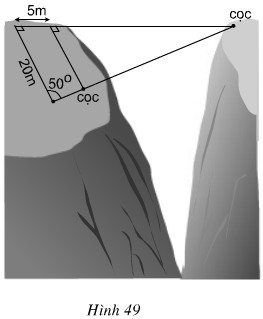
Tìm khoảng cách giữa hai cọc để căng dây vượt qua vực trong hình 49 (làm tròn đến mét)

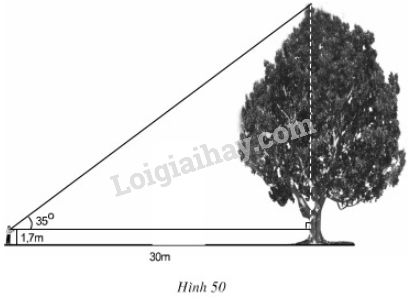
Tính chiều cao của cây trong hình 50 (làm tròn đến đề - xi – mét)

Tam giác ABC vuông tại \(C\) có \(AC = 2cm, BC = 5cm,\) \(\widehat {BAC} = x,\widehat {ABC} = y\). Dùng các thông tin sau (nếu cần) để tìm \(x – y\):

\(\sin 23°36’ ≈ 0,4;\)

\(\cos66°24’ ≈ 0,4;\)

\(tg21°48’ ≈ 0,4.\) 

Ở một cái thang dài \(3m\) người ta ghi: “ Để đảm bảo an toàn khi dùng thang phải đặt thang này tạo với mặt đất một góc có độ lớn từ \(60^0\) đến \(70^0\)”. Đo góc thì khó hơn đo độ dài. Vậy hãy cho biết: Khi dùng thang đó chân thang phải đặt cách tường bao nhiêu mét để đảm bảo an toàn.

Đố:

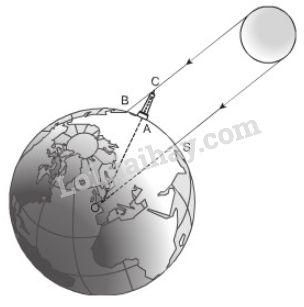
Vào khoảng năm 200 trước Công nguyên, Ơ-ra-tô-xten, một nhà Toán học và thiên văn học Hi Lạp, đã ước lượng được “chu vi” của Trái Đất (chu vi đường Xích Đạo) nhờ hai quan sát sau:

1) Một ngày trong năm, ông ta để ý thấy Mặt Trời chiếu thẳng các đáy giếng ở thành phố Xy-en (Nay gọi là Át–xu-an), tức là tia sáng chiếu thẳng đứng.

2) Cùng lúc đó ở thành phố A-lếch-săng-đri-a cách Xy-en 800km, một tháp cao 25m có bóng trên mặt đất dài 3,1m.

Từ hai quan sát trên, em hãy tính xấp xỉ “chu vi” Trái Đất.

(Trên hình 5, điểm S tượng trưng cho thành phố Xy-en, điểm A tượng trung cho thành phố A-lếch-xăng-đri-a, bóng của tháp trên mặt đất được coi là đoạn thẳng AB).

Bài 1. a. Không sử dụng máy tính, hãy sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần: \(sin{78^o},{\rm{ }}cos{24^o},{\rm{ }}sin{40^o},{\rm{ }}cos{87^o},{\rm{ }}sin{42^o}\)

b. Tính : \(D = {\sin ^2}15^\circ  + {\sin ^2}75^\circ  - {{2\cos 49^\circ } \over {\sin 41^\circ }} \)\(\,+ \tan 26^\circ .\tan 64^\circ \)

Bài 2. Cho tam giác ABC vuông tại A, đường cao AH, \(AC = 3cm,HC = 1,8cm.\)

a. Giải tam giác ABC

b. Tính độ dài phân giác AD của tam giác ABC (số đo góc làm tròn đến phút, độ dài đoạn thẳng làm tròn đến chữ số thập phân thứ hai)

Bài 3. Cho tam giác ABC nhọn, đường cao AH. Gọi M, N lần lượt là hình chiếu của H lên AB và AC.

a. Chứng minh \(AM.AB = AN.AC\).

b. Chứng minh \({{{S_{AMN}}} \over {{S_{ABC}}}} = {\sin ^2}B.{\sin ^2}C\)

Bài 1. Cho góc nhọn α, biết \(\cos \alpha  = {3 \over 4}\). Không tính số đo góc \(α\), hãy tính \(\sinα, \tanα, \cotα\).

Bài 2. Cho \(∆ABC\) có \(AB = 12cm, AC = 16cm, \)\(BC = 20cm.\)

a. Tính đường cao AH của ∆ABC

b. Chứng minh rằng: \(AB.\cos B + AC.\cos C = 20cm\)

Bài 3. Cho hình bình hành \(ABCD\) có AC là đường chéo lớn. Kẻ \(CH ⊥ AD (H ∈ AD)\) và \(CK ⊥ AB (K ∈ AB)\)

a. Chứng minh : \(∆CKH\) và \(∆ABC\) đồng dạng.

b. Chứng minh: \(HK = AC.\sin \widehat {BAD}\)

Bài 1. Không dùng bảng và máy tính, hãy tính:

\(A = {\sin ^2}10^\circ  + {\sin ^2}20^\circ  + ... + {\sin ^2}70^\circ  \)\(\;+ {\sin ^2}80^\circ \)

Bài 2. Cho tam giác ABC vuông tại A, biết \(AC = 12cm, BC = 15cm.\)

a. Giải tam giác vuông ABC.

b. Tính độ dài đường cao AH và đường phân giác AD của ∆ABC (số đo góc làm tròn đến độ, độ dài đoạn thẳng làm tròn đến chữ số thập phân thứ hai)

Bài 3. Cho hình bình hành ABCD có BD vuông góc với BC. Biết \(AB = a\), \(\widehat A = \alpha .\) Tính diện tích hình bình hành ABCD theo a và α.

Bài 4. Dựng góc \(α\), biết \(\tan α = 0,75\) (vẽ hình và nêu cách dựng).

Bài 1. Cho tam giác ABC cân tại A có \(AB = AC = 1\;cm\) và góc \(A = 2α (0 < α < 45^o)\), các đường cao AD và BE.

a. Chứng minh rằng : ∆ADC và ∆BEC đồng dạng

b. Chứng minh : \(\sin A = 2\sinα.\cosα\)

Bài 2. Cho ∆ABC vuông tại A và \(AC = 21cm\), \(\cos \widehat C = {3 \over 5}\)

a. Tính \(\tan B, \cot B\).

b. Đường phân giác của góc A cắt cạnh BC tại D. Tính \(DB, DC\)

Bài 1. Tính :

a. \(\left( {\cos 36^\circ  - \sin 36^\circ } \right).\left( {\cos 37^\circ  - \sin 38^\circ } \right).\left( {\cos 42^\circ  - \sin 48^\circ } \right)\)

b. \(\left( {\tan 52^\circ  + \cot 43^\circ } \right).\left( {\tan 29^\circ  + \cot 61^\circ } \right).\left( {\tan 13^\circ  - \tan 24^\circ } \right)\)

Bài 2. Cho tam giác ABC vuông tại A có \(AB = 6cm, BC = 10cm\), đường cao AH. Gọi E, F là hình chiếu của H lần lượt lên AB, AC.

a. Tính EF

b. Chứng minh rằng : \(AE.AB = AF.AC\)

c. Tính : \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\)

Bài 3. Cho tam giác ABC vuông tại A. Từ trung điểm E của cạnh AC, vẽ EF vuông góc với BC.

a. Chứng minh rằng : \(AF = BE.\cos C\).

b. Cho \(BC = 20cm; \sin C = 0,6\). Tính \({S_{AEFB}}\)

Bài 1. Tính giá trị của biểu thức :

\(A = {{3\cot 77^\circ } \over {2\tan 13^\circ }} - {{{{\cos }^2}26^\circ  + {{\cos }^2}64^\circ  - {{\cos }^2}71^\circ  - {{\cos }^2}19^\circ } \over {{{\sin }^2}34^\circ  + {{\sin }^2}56^\circ  + {{\sin }^2}15^\circ  + {{\sin }^2}75^\circ }}\)

Bài 2. Cho hình thang ABCD (AB // CD) có \(AB = 1cm\), \(CD = 5cm\) và \(\widehat C = 30^\circ ,\widehat D = 60^\circ \). Tính diện tích hình thang ABCD.

Bài 3. Cho tam giác ABC có ba góc nhọn, các đường cao BI, CK cắt nhau tại H. Trên đoạn HB, HC lần lượt lấy các điểm D và E sao cho \(\widehat {ADC} = \widehat {AEB} = 90^\circ .\)

a. Chứng minh rằng ∆ADE cân

b. Cho \(AD = 6cm, AC = 10cm\). Tính DC, CI và diện tích \(∆ADI.\)