Bài 45. Ảnh của một vật tạo bởi thấu kính phân kì

Hãy làm thí nghiệm để chứng tỏ rằng không thể hứng được ảnh của vật trên màn với mọi vị trí của vật?

Làm thế nào để quan sát được ảnh của vật tạo bởi thấu kính phân kì? Ảnh đó là ảnh thật hay ảnh ảo? Cùng chiều hay ngược chiều với vật?

Dựa vào kiến thức đã học ở bài trước, hãy nêu cách dựng ảnh của vật AB qua thấu kính phân kì, biết AB vuông góc với trục chính, A nằm trên trục chính.

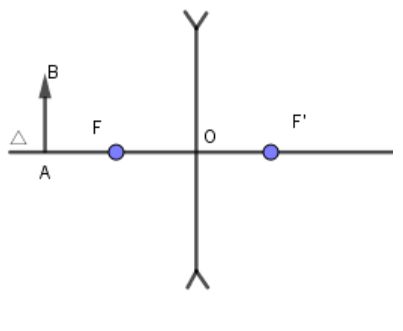
Trên hình 45.2 cho biết vật AB được đặt vuông góc với trục chính của thấu kính phân kì có tiêu cự f = 12cm. Điểm A nằm trên trục chính và cách quang tâm O một khoảng OA = 24cm.

+ Hãy dưng ảnh A'B' của vật AB tạo bởi thấu kính đã cho.

+ Dựa vào hình vẽ, hãy lập luận để chứng tỏ rằng ảnh này luôn nằm trong khoảng tiêu cự của thấu kính.

Đặt vật AB trước một thấu kính có tiêu cự f= 12cm. Vật AB cách thấu kính một khoảng d = 8cm, A nằm trên trục chính. Hãy dựng ảnh A'B' của AB. Dựa vào hình vẽ để nêu nhận xét về độ lớn của ảnh so với vật trong hai trường hợp:

+ Thấu kính là hội tụ.

+ Thấu kính là phân kì.

Từ bài toán trên, hãy cho biết ảnh ảo của một vật tạo bởi thấu kính hội tụ và thấu kính phân kì có đặc điểm gì giồng nhau, khác nhau. Từ đó hãy nên cách nhận biết nhanh chóng một thấu kính là hội tụ hay phân kì.

Vận dụng kiến thức hình học, tính khoảng cách từ ảnh đến thấu kính và chiều cao của ảnh trong hai trường hợp ở C5 khi vật có chiều cao h = 6mm.

Lại có: \(OB' = OB + BB'\)

Ta suy ra \(\left( 1 \right) \Leftrightarrow \dfrac{8}{{12}} = \dfrac{{BB'}}{{OB + BB'}}\)

\(\begin{array}{l} \Rightarrow \dfrac{{12}}{8} = \dfrac{{OB + BB'}}{{BB'}}\\ \Rightarrow 1,5 = \dfrac{{OB}}{{BB'}} + 1\end{array}\)

\( \Rightarrow \dfrac{{OB}}{{BB'}} = 0,5 \Rightarrow \dfrac{{BB'}}{{OB}} = 2\)  (2)

+ Ta có: \(\Delta OA'B' \sim \Delta OAB\)

Ta suy ra: \(\dfrac{{OA'}}{{OA}} = \dfrac{{A'B'}}{{AB}} = \dfrac{{OB'}}{{OB}}\)  (3)

Ta có \(OB' = OB + BB'\)

Ta suy ra \(\left( 3 \right) \Leftrightarrow \dfrac{{OA'}}{{OA}} = \dfrac{{A'B'}}{{AB}} = \dfrac{{OB + BB'}}{{OB}} = 1 + \dfrac{{BB'}}{{OB}}\)

Thế (2) vào (3) ta được: \(\dfrac{{OA'}}{{OA}} = \dfrac{{A'B'}}{{AB}} = 1 + 2 = 3\)

Từ đây ta suy ra:

- Khoảng cách từ ảnh đến thấu kính: \(OA' = 3.OA = 3.8 = 24cm\)

- Chiều cao của ảnh: \(A'B' = 3.AB = 3.6 = 18mm\)

Vậy ảnh có chiều cao \(18mm\) (cao gấp 3 lần vật) cách thấu kính một khoảng là \(24cm\)

+ Trường hợp 2: Thấu kính phân kì

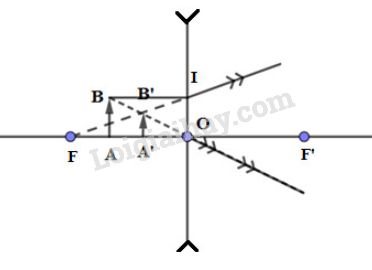
+ Ta có: \(\Delta IB'B \sim \Delta FB'O\)

Ta suy ra: \(\dfrac{{IB}}{{FO}} = \dfrac{{B'B}}{{B'O}}\)

Theo đầu bài ta có: \(IB = AO = 8cm\) và \(FO = 12cm\)

Ta suy ra: \(\dfrac{8}{{12}} = \dfrac{{B'B}}{{B'O}} \Rightarrow \dfrac{{B'B}}{{B'O}} = \dfrac{2}{3}\)  (1)

+ Ta có: \(\Delta OAB \sim \Delta OA'B'\)

Ta suy ra: \(\dfrac{{OA}}{{OA'}} = \dfrac{{OB}}{{OB'}} = \dfrac{{AB}}{{A'B'}}\)  

Lại có: \(OB = OB' + BB'\)

Ta suy ra: \(\dfrac{{OA}}{{OA'}} = \dfrac{{AB}}{{A'B'}} = \dfrac{{OB' + BB'}}{{OB'}} = 1 + \dfrac{{BB'}}{{OB'}}\) (2)

Từ (1) và (2) ta suy ra: \(\dfrac{{OA}}{{OA'}} = \dfrac{{AB}}{{A'B'}} = 1 + \dfrac{2}{3} = \dfrac{5}{3}\)

Từ đây, ta suy ra:

- Khoảng cách từ ảnh đến thấu kính: \(OA' = \dfrac{{OA}}{{\dfrac{5}{3}}} = \dfrac{8}{{\dfrac{5}{3}}} = 4,8cm\)

- Chiều cao của ảnh: \(A'B' = \dfrac{{AB}}{{\dfrac{5}{3}}} = \dfrac{6}{{\dfrac{5}{3}}} = 3,6mm\)

Vậy, ảnh có chiều cao \(3,6mm\) (cao gấp \(0,6\) lần vật) và cách thấu kính một khoảng là \(4,8cm\)

Hãy trả lời câu hỏi nêu ra ở phần mở bài?