Câu 1.Phát biểu mệnh đề đảo: “ Nếu một tam giác có hai đường cao bằng nhau thì tam giác đó là tam giác cân’.
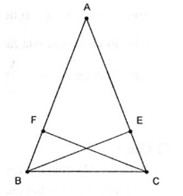
Chứng minh: Cho tam giác ABC có hai đường cao BE và CF bằng nhau.
Hai tam giác vuông BCF và CBE có cạnh BC chung và \(CF=BE\) nên bằng nhau. Suy ra \(\widehat {ABC} = \widehat {CBA}\).
Vậy ABC là tam giác cân tại A.
Câu 2.
Giả sử có số tự nhiên n sao cho n2 chia hết cho 3 và n không chia hết cho 3.
Đặt .
Khi đó: \({n^2} = {\left( {3k \pm 1} \right)^2} = 9{k^2} \pm 6k + 1\)\(\, = 3\left( {3{k^2} \pm 2k} \right) + 1\) .
Suy ra n2 không chia hết cho 3. Điều này trái với giả thiết.
Vậy với mọi số nguyên dương n, nếu n2 chia hết cho 3 thì n chia hết cho 3.
Câu 3.
a.
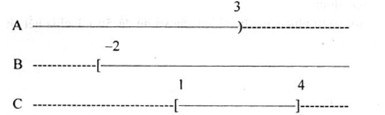
b.
+ \(A \cap B \cap C = \left[ {1;3} \right)\)
+ \(A\backslash B = \left( { - \infty ; - 2} \right)\)
+ \(B\backslash A = \left[ {3; + \infty } \right)\)
Câu 4.
Do \(\left\{ {1;2} \right\} \subset X\) nên \(1 \in X,2 \in X\) .
Do \(X \subset \left\{ {1;2;3;4;5} \right\}\) nên X có thể chưa thêm các phần tử 3, 4, 5.
Vậy X là các tập sau: \(\left\{ {1;2} \right\},\left\{ {1;2;3} \right\},\left\{ {1;2;4} \right\},\left\{ {1;2;5} \right\},\)\(\,\left\{ {1;2;3;4} \right\},\left\{ {1;2;3;5} \right\},\left\{ {1;2;4;5} \right\},\)\(\,\left\{ {1;2;3;4;5} \right\}\) .
Bài toán có 8 nghiệm.
Câu 5.
Ta có \({\left( {1,7321} \right)^2} = 3,00017041 > 3.\) Suy ra \(1,7321 > \sqrt 3 \) .
Tương tự \({\left( {1,7320} \right)^2} = 2,99982400 < 3.\) Suy ra \(1,7320 < \sqrt 3 \) .
Do đó \(0 > \sqrt 3 - 1,7321 > 1,7320 - 1,7321\)\(\, = - 0,0001\) .
Suy ra \({\Delta _a} = \left| {\overline a - a} \right| < 0,0001\) .
Vậy độ chính xác của sai số tuyệt đối là \(d= 0,0001.\)
Sai số tương đối \({\delta _a} = \dfrac{{{\Delta _a}}}{{\left| a \right|}} < \dfrac{d}{{\left| a \right|}} \approx 0,0005773 \)\(\,\approx 0,058\% {\text{ }}\)