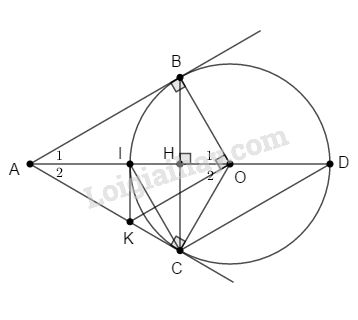
a. Ta có: \(OB = OC\; (=R)\) nên ∆BOC cân tại O có đường cao OH đồng thời là đường phân giác hay \({\widehat O_1} = {\widehat O_2}\)
Xét ∆OCA và ∆OBA có:
+) \(OA\) cạnh chung
+) \({\widehat O_1} = {\widehat O_2}\) (cmt)
+) \(OC = OB\; (= R)\)
Vậy \(∆OCA = ∆OBA\) (c.g.c)
\( \Rightarrow \widehat {OCA} = \widehat {OBA} = 90^\circ \)
\(⇒ AC\) là tiếp tuyến của (O)
b. Ta có: \(KO ⊥ OB, AB ⊥ OB\) (gt) \(⇒ KO // AB\)
\( \Rightarrow \widehat {KOA} = \widehat {BAO}\) (so le trong)
mà \(\widehat {BAO} = \widehat {KAO}\) (tính chất hai tiếp tuyến cắt nhau)
\( \Rightarrow \widehat {KOA} = \widehat {KAO} \Rightarrow KA = KO\)
c. ∆AKO cân (cmt) có KI là đường trung tuyến \(\left( {IA = IO = {{AO} \over 2} = {{2R} \over 2} = R} \right)\) nên đồng thời là đường cao hay \(KI ⊥ AO\). Chứng tỏ KI là tiếp tuyến của (O).
∆ABO vuông tại B có \(OA = 2R, OB = R\) (gt) nên là nửa tam giác đều
\( \Rightarrow {\widehat A_1} = 30^\circ \Rightarrow {\widehat A_2} = {\widehat A_1} = 30^\circ \) (tính chất tiếp tuyến cắt nhau)
∆AKI có \({\widehat A_2} = 30^\circ ,AI = R\) nên ta có \(IK = AI.\tan 30^\circ = {{R\sqrt 3 } \over 3}\)
d. ∆ACO vuông tại C, ta có:
\(AC = \sqrt {A{O^2} - O{C^2}} \)\(\; = \sqrt {{{\left( {2R} \right)}^2} - {R^2}} = R\sqrt 3 \)
Xét ∆AIC và ∆ACD có \(\widehat {CAI}\) chung và \({{AI} \over {AC}} = {{AC} \over {AD}} = {1 \over {\sqrt 3 }}\) nên:
∆AIC đồng dạng ∆ACD (c.g.c) \( \Rightarrow AI.AD = A{C^2} = {\left( {R\sqrt 3 } \right)^2} = 3{R^2}\) không đổi.
Cách khác: Ta có \(\widehat {ICO} = \widehat {DIC} \Rightarrow \widehat {ACI} = \widehat {ADC}\) ⇒ ∆AIC đồng dạng ∆ACD (g.g)