Bài 6. Tính chất của hai tiếp tuyến cắt nhau

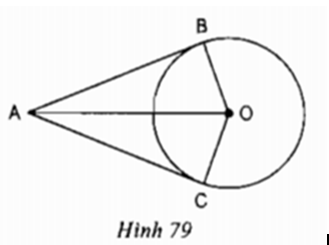
Cho hình 79 trong đó AB, AC theo thứ tự là các tiếp tuyến tại B, tại C của đường tròn (O). Hãy kể tên một vài đoạn thẳng bằng nhau, một vài góc bằng nhau trong hình.

Hãy nêu cách tìm tâm của một miếng gỗ hình tròn bằng “thước phân giác” (xem hình vẽ trong khung ở đầu bài 6).

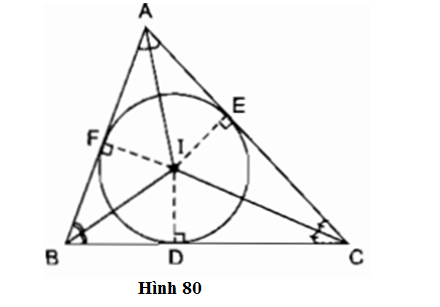
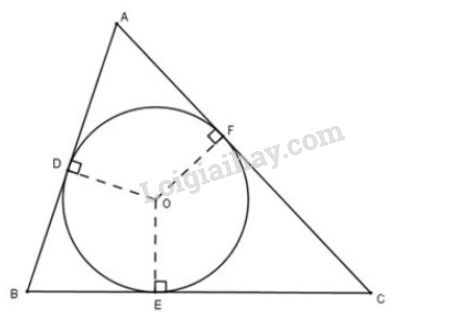
Cho tam giác ABC. Gọi I là giao điểm của các đường phân giác các góc trong của tam giác; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ I đến các cạnh BC, AC, AB (h.80). Chứng minh rằng ba điểm D, E, F nằm trên cùng một đường tròn tâm I. 

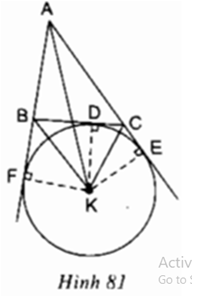
Cho tam giác ABC, K là giao điểm các đường phân giác của hai góc ngoài tại B và C; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ K đến các đường thẳng BC, AC, AB (h.81). Chứng minh rằng ba điểm D, E, F năm trên cùng một đường tròn có tâm K.

Cho đường tròn \((O)\), điểm \(A\) nằm bên ngoài đường tròn. Kẻ các tiếp tuyến \(AB,\ AC\) với đường tròn (\(B,\ C\) là các tiếp điểm).

a) Chứng minh rằng \(OA\) vuông góc với \(BC\).

b) Vẽ đường kính \(CD\). Chứng minh rằng \(BD\) song song với \(AO\).

c) Tính độ dài các cạnh của tam giác \(ABC\); biết \(OB=2cm,\ OA=4cm\).

Từ một điểm \(A\) nằm bên ngoài đường tròn \((O)\), kẻ các tiếp tuyến \(AB,\ AC\) với đường tròn (\(B,\ C\) là các tiếp điểm). Qua điểm \(M\) thuộc cung nhỏ \(BC\), kẻ tiếp tuyến với đường tròn \(O\), nó cắt các tiếp tuyến \(AB\) và \(AC\) theo thứ tự ở \(D\) và \(E\). Chứng minh rằng chu vi tam giác \(ADE\) bằng \(2AB\). 

Cho góc \(xAy\) khác góc bẹt. Tâm của các đường tròn tiếp xúc với hai cạnh của góc \(xAy\) nằm trên đường nào?

Cho góc \(xAy\) khác góc bẹt, điểm \(B\) thuộc \(Ax\). Hãy dựng đường tròn \((O)\) tiếp xúc với \(Ax\) tại \(B\) và tiếp xúc với \(Ay\).

Cho nửa đường tròn tâm \(O\) có đường kính \(AB\) (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi \(Ax,\ By\) là các tia vuông góc với \(AB\) (\(Ax,\ By\) và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ \(AB\)). Qua điểm \(M\) thuộc nửa đường tròn (\(M\) khác \(A\) và \(B\)), kẻ tiếp tuyến với nửa đường tròn, nó cắt \(Ax\) và \(By\) theo thứ tự ở \(C\) và \(D\).

Chứng minh rằng: 

a) \(\widehat {CO{\rm{D}}} = {90^0}\)

b) \(CD=AC+BD\)

c) Tích \(AC.BD\) không đổi khi điểm \(M\) di chuyển trên nửa đường tròn.

Trên hình \(82\), tam giác \(ABC\) ngoại tiếp đường tròn \((O)\).

a) Chứng minh rằng:

\(2AD=AB+AC-BC.\)

b) Tìm các hệ thức tương tự hệ thức ở câu a).

Cho tam giác đều \(ABC\) ngoại tiếp đường tròn bán kính \(1cm\). Diện tích của tam giác \(ABC\) bằng:

(A) \(6cm^{2}\);

(B) \(\sqrt{3}cm^{2}\);

(C) \(\dfrac{3\sqrt{3}}{4}cm^{2}\)

(D) \(3\sqrt{3}cm^{2}.\)

Hãy chọn câu trả lời đúng.

Cho đường tròn (O; R) và một điểm A sao cho \(OA = 2R.\) Vẽ các tiếp tuyến AB, AC (B, C là các tiếp điểm). Đường thẳng OA cắt BC tại H, cắt cung nhỏ và cung lớn BC lần lượt tại M và N.

a. Chứng minh rằng: \(OA ⊥ BC\) và \({R^2} = OA.HM\)

b. Vẽ cát tuyến bất kì ADE. Gọi K là trung điểm của DE. Chứng tỏ năm điểm A, B, O, K, C thuộc cùng một đường tròn.

Cho góc \(\widehat {xOy} = 60^\circ .\) Đường tròn tâm K bán kính R tiếp xúc với Ox tại A và Oy tại B. Từ điểm M trên cung nhỏ AB, vẽ tiếp tuyến với đường tròn, tiếp tuyến này cắt Ox, Oy lần lượt tại C và D.

a. Tính chu vi ∆COD theo R. Chứng tỏ chu vi đó không đổi khi M chạy trên cung nhỏ AB.

b. Chứng minh số đo \(\widehat {CKD}\) không đổi khi M chạy trên cung nhỏ AB.

Cho nửa đường tròn (O; R) đường kính AB. Kẻ các tiếp tuyến tại A và B với nửa đường tròn. Qua điểm M thuộc nửa đường tròn (M khác A và B) kẻ tiếp tuyến thứ ba cắt các tiếp tuyến tại A và B lần lượt tại C và D.

a. Chứng minh rằng : \(CD = CA + BD\); \(\widehat {COD} = 90^\circ \)

b. Chứng minh AB là tiếp tuyến của đường tròn đường kính CD.

Cho đường tròn (O) đường kính AB. Lấy điểm C thuộc (O), tiếp tuyến A của (O) cắt BC tại D. Gọi M là trung điểm của AD.

a. Chứng minh MC là tiếp tuyến của (O).

b. Chứng minh \(MO ⊥ AC\) tại trung điểm I của AC.

Cho nửa đường tròn (O) đường kính AB. M là điểm bất kì thuộc nửa đường tròn. Kẻ MH ⊥ AB (H ∈ AB). Vẽ đường tròn (M; MH). Kẻ các tiếp tuyến AC, BD với đường tròn (M) (C, D là các tiếp điểm)

a. Chứng minh ba điểm C, M, D thẳng hàng và CD là tiếp tuyến của (O)

b. Chứng minh rằng khi M di chuyển trên (O) thì AC + BD không đổi.

Từ điểm P nằm ngoài đường tròn (O; R), vẽ hai tiếp tuyến PA, PB (A, B là các tiếp điểm). Gọi H là chân đường vuông góc kẻ từ A đến đường kính BC. Chứng minh rằng PC cắt AH tại trung điểm I của AH.

Từ điểm M ở ngoài đường tròn (O; R), kẻ đường thẳng qua O cắt đường tròn ở hai điểm A và B.

a. Chứng minh rằng : \(MA.MB = M{O^2} - {R^2}\)

b. Kẻ cát tuyến thứ hai MCD với đường tròn. Chứng minh: \(MC.MD = MA.MB.\)

Cho nửa đường tròn tâm O đường kính AB. Trên cùng nửa mặt phẳng có bờ là đường thẳng AB, vẽ các tiếp tuyến Ax, By với (O) (A, B là các tiếp điểm). Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt Ax, By lần lượt tại C và D. Gọi N là giao điểm của AD và BC. Chứng minh:

a. \(CD = CA + DB\)

b. \(MN ⊥ AB.\)

Cho tam giác ABC. Gọi O₁, O₂, O₃ là tâm các đường tròn bàng tiếp cỉa tam giác ABC. Chứng minh rằng A, B, C là chân các đường cao của tam giác O₁O₂O₃.

Một đường thẳng d cố định nằm ngoài đường tròn (O; R). Lấy M bất kì trên d. Từ M kẻ hai tiếp tuyến MP và MQ đến đường tròn (O) (P, Q là các tiếp điểm). Kẻ \(OH ⊥ d\). Dây cung PQ cắt OH ở I, cắt OM ở K. Chứng minh rằng :

a. \(OH.OI = OM.OK = {R^2}\)

b. Khi M thay đổi trên đường thẳng d thì  vị trí của điểm I luôn luôn cố định.