Bài 1:
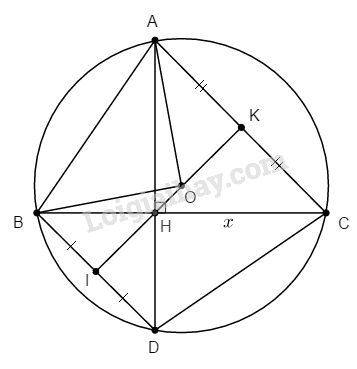
a) \(\widehat C = 45^\circ (gt) \Rightarrow \widehat {AOB} = 90^\circ .\) Do đó \(AB = R\sqrt 2 \)
\(\widehat B = 60^\circ (gt) \Rightarrow AC = R\sqrt 3 \)
∆AHB vuông có \(\widehat B = 60^\circ \) và \(AB = R\sqrt 2 \)
\( \Rightarrow HB = AB.\cos 60^\circ = {{R\sqrt 2 } \over 2}\)
Đặt \(HC = x\), ta có :
\(H{C^2} + {\rm{ }}H{A^2} = {\rm{ }}A{C^2}\) hay \({x^2} + {\rm{ }}{x^2} = {\left( {R\sqrt 3 } \right)^2}\)
\(2{x^2} = 3{R^2} \Rightarrow x = {{R\sqrt 3 } \over {\sqrt 2 }} = {{R\sqrt 6 } \over 2}\)
Do đó \(BC = BH + HC = {{R\sqrt 2 } \over 2} + {{R\sqrt 6 } \over 2}\)\(\; = {{R\sqrt 2 \left( {1 + \sqrt 3 } \right)} \over 2}\).
b) Ta có ∆AHC vuông tại H, có \(\widehat {ACH} = 45^\circ \)(gt) \(\Rightarrow\) ∆AHC vuông cân
Mặt khác \(\widehat {DBC} = \widehat {DAC} = 45^\circ \)(góc nội tiếp cùng chắn )
\( \Rightarrow \widehat {ACB} = \widehat {CBD} = 45^\circ \)
Do đó AC // BD ( cặp góc so le trong bằng nhau)
Vậy ABDC là hình thang có bốn đỉnh A, B, D, C thuộc đường tròn nên ABDC là hình thang cân.
Ta có ∆AHB vuông tại H, có \(\widehat B = 60^\circ \Rightarrow \widehat {BAD} = 30^\circ \).
Do đó \(\widehat {BOD} = 60^\circ \) (góc nội tiếp bằng nửa góc ở tâm cùng chắn một cung) \(\Rightarrow\) ∆BOD đều.
\(BD = R\). Gọi \(IK\) là trục đối xứng của hình thang cân ABDC, ta có :
\(OI = {{R\sqrt 3 } \over 2},OK = {R \over 2}\) ( vì ∆AOC cân có \(\widehat {AOC} = 120^\circ \) )
Do đó \(IK = IO + OK = {{R\sqrt 3 } \over 2} + {R \over 2} \)\(\;= {{R\left( {\sqrt 3 + 1} \right)} \over 2}\)
Vậy \({S_{ABDC}} = {{\left( {AC + BD} \right).IK} \over 2}\)\(\; = {{\left( {R\sqrt 3 + R} \right).{{R\left( {\sqrt 3 + 1} \right)} \over 2}} \over 2} = {{{R^2}\left( {2 + \sqrt 3 } \right)} \over 2}\) .
c) Đường IK là trục đối xứng của hình thang ABDC. Khi quay hình thang cân ABDC một vòng quanh IK ta được hình sinh ra là hình nón cụt có bán kính đáy lớn là \({{AC} \over 2} = {{R\sqrt 3 } \over 2}\), đáy nhỏ là \({{BD} \over 2} = {R \over 2}\) và đường cao \(IK = {{R\left( {\sqrt 3 + 1} \right)} \over 2}\).
Vậy thể tích của hình là :
\(V = {1 \over 3}\pi h.\left( {R_1^2 + R_2^2 + {R_1}{R_2}} \right) \)
\(= {1 \over 3}\pi .IK.\left[ {{{\left( {{{AC} \over 2}} \right)}^2} + {{\left( {{{BD} \over 2}} \right)}^2} + {{AC} \over 2}.{{BD} \over 2}} \right]\)
\(={1 \over 3}\pi .{{R\left( {\sqrt 3 + 1} \right)} \over 2}.\left[ {{{\left( {{{R\sqrt 3 } \over 2}} \right)}^2} + {{\left( {{R \over 2}} \right)}^2} + {{R\sqrt 3 } \over 2}.{R \over 2}} \right]\)
\(={1 \over 3}\pi .{{R\left( {\sqrt 3 + 1} \right)} \over 2}\left[ {{{3{R^2} + {R^2} + {R^2}\sqrt 3 } \over 4}} \right]\)
\(={1 \over 6}\pi R\left( {\sqrt 3 + 1} \right).{{{R^2}\left( {4 + \sqrt 3 } \right)} \over 4} \)
\(= {1 \over {24}}\pi {R^3}\left( {\sqrt 3 + 1} \right)\left( {4 + \sqrt 3 } \right)\).
Bài 2: Chi tiết máy gồm hai hình trụ :
\(10 : 2 = 5\) (đvđd)
\(4 : 2 = 2 \) (đvđd).
Gọi S1, S2 lần lượt là diện tích bề mặt của hình trụ thứ nhất và hình trụ thứ hai, ta có :
\({S_1} = 2\pi {R_1}{h_1} + 2\pi R_1^2\)\(\; = 2\pi .5.2 + 2\pi {.5^2} = 70\pi \) (đvdt)
\({S_2} = 2\pi {R_2}{h_2} + 2\pi R_2^2 \)\(\;= 2\pi .2.5 + 2\pi {.2^2} = 28\pi \) (đvdt)
Vậy diện tích bề mặt của chi tiết máy \({S_1} + {S_2} - \pi R_2^2 = 94\pi \) (đvdt)
Tương tự, gọi V1, V2 lần lượt là thể tích của hình trụ thứ nhất và hình trụ thứ hai, ta có : \({V_1} = \pi R_1^2{h_1} = \pi {.5^2}.2 = 50\pi \) (đvdt)
\({V_2} = \pi R_2^2{h_2} = \pi {.2^2}.5 = 20\pi \) (đvdt)
Vậy thể tích của chi tiết máy là \({V_1} + {\rm{ }}{V_2} = 50\pi + 20\pi = 70\pi \) (đvdt).