Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương 4 - Hình học 9

Cho nửa đường tròn (O; R) đường kính AB. Từ điểm M trên nửa đường tròn kẻ tiếp tuyến thứ ba cắt hai tiếp tuyến Ax và By tại C và D.

a)      Chứng minh rằng tích AC.BD không đổi, không phụ thuộc vào vị trí của điểm M.

b)     Cho \(AC = {R \over 2}.\)

Quanh cạnh đáy AB. Hãy tính thể tích hình được sinh ra do diện tích giới hạn bởi nửa đường tròn đường kính AB và hình thang vuông ACDB.

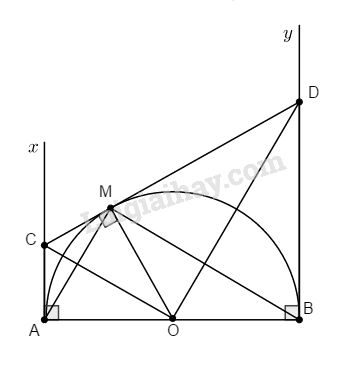
a)Ta có CO là phân giác của \(\widehat {AOM}\) (tính chất hai tiếp tuyến cắt nhau)

Tương tự OD là phân giác của \(\widehat {MOB}\) mà \(\widehat {AOM} + \widehat {MOB} = 180^\circ \)

\( \Rightarrow \widehat {COD} = 90^\circ \) nên ∆COD vuông tại O có đường cao OM ta có

\(MC.MD = MO^2= R^2\) mà \(MC = AC, MD = BD\) (tính chất hai tiếp tuyến cắt nhau)

\(\Rightarrow AC.BD = R^2\)                        (1) không đổi.

b)    

Dễ thấy tứ giác ACMO nội tiếp ( vì \(\widehat {CAO} + \widehat {CMO} = 180^\circ \))

\( \Rightarrow \widehat {MCO} = \widehat {MAO}\) ( góc nội tiếp cùng chắn)

Tương tự ta có tứ giác BDMO nội tiếp \( \Rightarrow \widehat {MDO} = \widehat {MBO}\)

Do đó ∆COD và ∆AMB đồng dạng (g.c.g)   \( \Rightarrow {{{S_{COD}}} \over {{S_{AMB}}}} = {\left( {{{CD} \over {AB}}} \right)^2}\)

Ta tính CD theo R : Từ (1)   \( \Rightarrow BD = {{{R^2}} \over {AC}} = {{{R^2}} \over {{R \over 2}}} = 2R\)

Do đó  \(DM = BD = 2R.\)

Ta có \(CD = CM + DM = {R \over 2} + 2R = {{5R} \over 2}\)

Vậy \({{{S_{COD}}} \over {{S_{AMB}}}} = {\left( {{{5R} \over 2}} \right)^2}:{\left( {2R} \right)^2} = {{25} \over {16}}.\)

Do Ax, By là hai tiếp tuyến của (O) nên Ax // By ( vì cùng vuông góc với  AB) nên ACDB là hình thang vuông.

Khi cho hình thang quay quanh cạnh đáy AB thì thể tích của hình được sinh ra do giới hạn bởi nửa đường tròn đường kính AB và  hình thang ACDB là hiệu giữa thể tích hình nón cụt có đáy lớn \(BD = 2R\), đáy nhỏ \(AC = {R \over 2}\), chiều cao \(AB = 2R\) và thể tích hình cầu tâm O bán kính R.

Gọi V_n là thể tích của hình nón cụt.

\({V_n} = {1 \over 3}\pi \left( {{R^2} + r + R.r} \right).h \)

\(\;\;\;\;\;= {1 \over 3}\pi \left( {B{D^2} + A{C^2} + BD.AC} \right).AB\)

\(\;\;\;\;\;={1 \over 3}\pi \left[ {{{\left( {2R} \right)}^2} + {{\left( {{R \over 2}} \right)}^2} + 2R.{R \over 2}} \right].2R \)

\(\;\;\;\;\;= {2 \over 3}\pi R\left( {4{R^2} + {{{R^2}} \over 4} + {R^2}} \right) = {{7\pi {R^3}} \over 2}\)

Gọi V_c là thể tích hình cầu : \({V_c} = {4 \over 3}\pi {R^3}\)

và V là thể tích cần tìm : \(V = {V_n} - {V_c} = {{7\pi {R^3}} \over 2} - {4 \over 3}\pi {R^3} = {{13\pi {R^3}} \over 6}\).