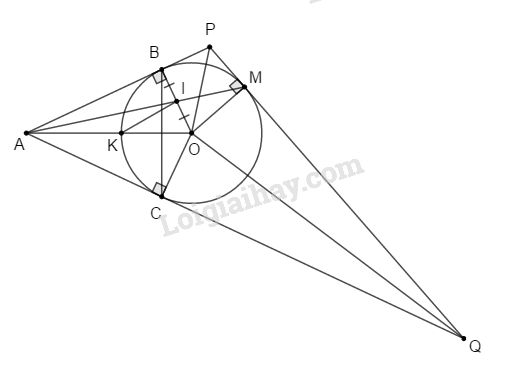
a. Ta có: \(AB = AC\) (tính chất hai tiếp tuyến cắt nhau)
\(OB = OC (= R).\)
Do đó AO là đường trung trực của đoạn BC.
Ta có: \(AB ⊥ OB\) (tính chất tiếp tuyến)
\(⇒ ∆ABO\) vuông tại B, theo định lí Pi-ta-go, ta có:
\(AB = \sqrt {A{O^2} - B{O^2}} = \sqrt {{{\left( {2R} \right)}^2} - {R^2}} \)\(\,= R\sqrt 3 \)
b. Ta có: IK là đường trung bình của ∆AOB nên:
\(IK = {1 \over 2}AB = {{R\sqrt 3 } \over 2}\) và IK // AB, mà \(AB ⊥ OB ⇒ IK ⊥ OB.\)
Ta có: \({S_{OIK}} = {1 \over 2}IK.IO = {1 \over 2}.{{R\sqrt 3 } \over 2}.{R \over 2} = {{{R^2}\sqrt 3 } \over 8}\) (đvdt)
c. Ta có:
\(\eqalign{ p - AQ &= {{AP + PQ + AQ} \over 2} - AQ\cr& = {{AP + PQ + AQ - 2AQ} \over 2} \cr & = {{AP + PQ - AQ} \over 2} \cr&= {{AB + BP + PM + MQ - CQ - AC} \over 2} \cr & = {{BP + PM} \over 2} = {{2PM} \over 2} \cr&= PM\,\left( {đpcm} \right) \cr} \)
d. Ta có:
\(\eqalign{ & {S_{APQ}} = {S_{AOQ}} + {S_{QOP}} + {S_{POA}} \cr & = {1 \over 2}R.AQ + {1 \over 2}R.QP + {1 \over 2}R.AP \cr&= {1 \over 2}R\left( {AQ + QP + AP} \right) \cr} \)