a) (hình bên)
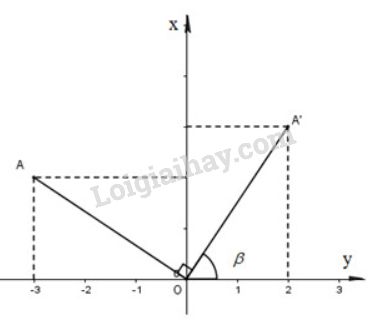
Phép quay tâm góc \(-90^0\) biến điểm M(x;y) thành điểm M'(x';y') với \(\left\{ \begin{array}{l}x' = x\cos \left( { - {{90}^0}} \right) - y\sin \left( { - {{90}^0}} \right) = y\\y' = x\sin \left( { - {{90}^0}} \right) + y\cos \left( { - {{90}^0}} \right) = - x\end{array} \right.\)
\( \Rightarrow A'\left( {2;3} \right);\,\,B'\left( {5;4} \right);\,\,C'\left( {3;1} \right)\) lần lượt là ảnh của A, B, C qua phép quay tâm O, góc quay \(-90^0\).
b) (Hình 1.26)
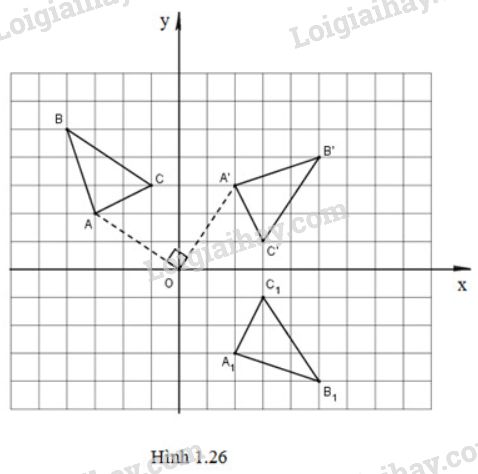
Gọi tam giác \({A_{1}}^{}\)\({B_{1}}^{}\)\({C_{1}}^{}\) là ảnh của tam giác \(A'B'C'\) qua phép đối xứng trục \(Ox\). Khi đó \({A_{1}}^{}\)(2;-3), \({B_{1}}^{}\) (5;-4), \({C_{1}}^{}\)(3;-1) là đáp số cần tìm.