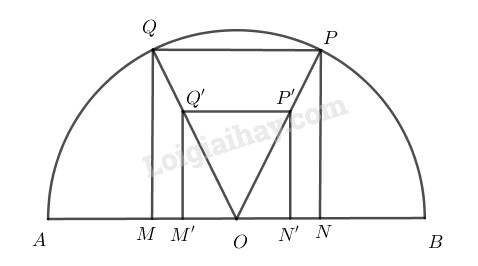
Gọi \(O\) là trung điểm của\(AB\). Giả sử dựng được hình vuông \(MNPQ\) có \(M\), \(N\) thuộc đường kính \(AB\), \(P\), \(Q\) thuộc nửa đường tròn. Khi đó \(O\) phải là trung điểm của \(MN\). Nếu lấy một hình vuông \(M’N’P’Q’\) sao cho \(M’\), \(N’\) thuộc \(AB\), \(O\) là trung điểm của \(M’N’\) khi đó ta thấy \(\dfrac{OM}{OM’}=\dfrac{ON}{ON’}=\dfrac{OP}{OP’}=\dfrac{OQ}{OQ’}\)
Từ đó suy ra hình vuông \(MNPQ\) là ảnh của hình vuông \(M’N’P’Q’\) qua phép vị tự tâm \(O\), suy ra \(O\), \(P\), \(P’\) và \(O\), \(Q\), \(Q’\) thẳng hàng.
Vậy ta có cách dựng:
- Dựng hình vuông \(M’N’P’Q’\) nằm trong nửa hình tròn đã cho sao cho \(M’N’\) thuộc \(AB\) và \(O\) là trung điểm của \(M’N’\). Tia \(OP’\) cắt nửa đường tròn tại \(P\); tia \(OQ’\) cắt nửa đường tròn tại \(Q\) .
Khi đó dễ thấy tứ giác \(MNPQ\) là hình vuông cần dựng.