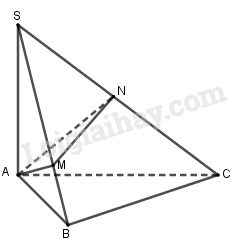
Ta có: \(SC \bot \left( {AMN} \right) \Rightarrow \left\{ \begin{array}{l}SC \bot AM\\SC \bot MN\end{array} \right.\).
Tam giác \(ABC\) có \(A{C^2} = A{B^2} + B{C^2}\) nên vuông tại \(B\).
Suy ra \(AB \bot BC\), mà \(SA \bot BC\) nên \(BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\).
Tam giác \(SMN\) đồng dạng tam giác \(SCB\) (g.g) \( \Rightarrow \dfrac{{{S_{SMN}}}}{{{S_{SCB}}}} = {\left( {\dfrac{{SN}}{{SB}}} \right)^2}\)
Tam giác \(SAC\) vuông cân tại \(A\) có \(AN \bot SC\) \( \Rightarrow SN = \dfrac{1}{2}SC = \dfrac{1}{2}\sqrt {{5^2} + {5^2}} = \dfrac{{5\sqrt 2 }}{2}\).
Tam giác \(SAB\) có \(SA = 5,AB = 3 \Rightarrow SB = \sqrt {34} \)
\( \Rightarrow \dfrac{{{S_{SMN}}}}{{{S_{SCB}}}} = {\left( {\dfrac{{SN}}{{SB}}} \right)^2} = \dfrac{{25}}{{68}}\)\( \Rightarrow \dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \dfrac{{25}}{{68}}\).
Mà \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}.5.\dfrac{1}{2}.3.4 = 10\) nên \({V_{S.AMN}} = \dfrac{{25}}{{68}}.10 = \dfrac{{125}}{{34}}\).
Chọn B.