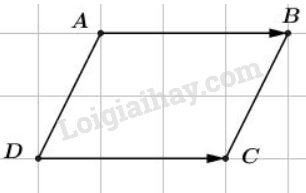
Ta chứng minh hai mệnh đề:
*) Khi \(\overrightarrow{AB}= \overrightarrow{DC}\) thì \(ABCD\) là hình bình hành.
Thật vậy, theo định nghĩa của vec tơ bằng nhau thì:
\(\overrightarrow{AB} = \overrightarrow{DC} ⇔ \left | \overrightarrow{AB} \right |= \left | \overrightarrow{DC} \right |\) và \(\overrightarrow{AB}\) và \(\overrightarrow{DC}\) cùng hướng.
\(\overrightarrow{AB}\) và \(\overrightarrow{DC}\) cùng hướng suy ra \(\overrightarrow{AB}\) và \(\overrightarrow{DC}\) cùng phương, suy ra giá của chúng song song với nhau,
hay \(AB // DC\) (1)
Ta lại có \(\left | \overrightarrow{AB} \right |= \left | \overrightarrow{DC} \right |\) suy ra \(AB = DC\) (2)
Từ (1) và (2), theo dấu hiệu nhận biết hình bình hành, tứ giác \(ABCD\) có một cặp cạnh song song và bằng nhau nên nó là hình bình hành.
*) Khi \(ABCD\) là hình bình hành thì \(\overrightarrow{AB} = \overrightarrow{DC}\)
Khi \(ABCD\) là hình bình hành thì \(AB // CD.\) Dễ thấy, từ đây ta suy ra hai vec tơ \(\overrightarrow{AB}\) và \(\overrightarrow{DC}\) cùng hướng (3)
Mặt khác \(AB = DC\) suy ra \(\left | \overrightarrow{AB} \right |\) = \(\left | \overrightarrow{DC} \right |\) (4)
Từ (3) và (4) suy ra \(\overrightarrow{AB}= \overrightarrow{DC}.\)
Như vậy tứ giác \(ABCD\) là hình bình hành khi và chỉ khi \(\overrightarrow{AB}= \overrightarrow{DC}.\)