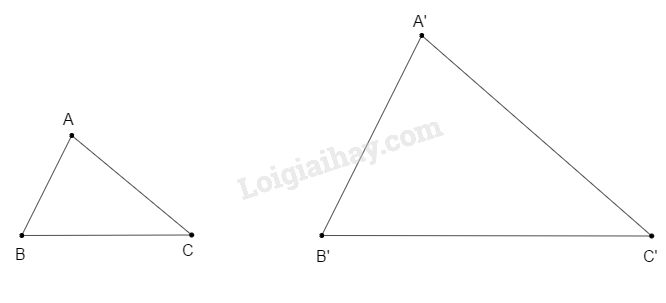
\( \Rightarrow \Delta ABC \) đồng dạng \( \Delta A'B'C'\left( {gt} \right)\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{{AB}}{{A'B'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{{BC}}{{B'C'}}\)\(\, = \dfrac{{AB + AC + BC}}{{A'B' + A'C' + B'C'}}\) \( = \dfrac{{{C_{ABC}}}}{{{C_{A'B'C'}}}}\)
hay \(\dfrac{3}{A'B'}\) = \(\dfrac{7}{B'C'}\) = \(\dfrac{5}{A'C'}\) = \(\dfrac{C_{ABC}}{55}\) = \(\dfrac{3 + 7 + 5}{55}\) = \(\dfrac{{15}}{{55}}\) = \(\dfrac{3}{11}\)
\( + )\,\,\dfrac{3}{{A'B'}} = \dfrac{3}{{11}}\)\(\; \Rightarrow A'B' = \dfrac{{3.11}}{3} = 11\,cm\)
\( + )\,\,\dfrac{7}{{B'C'}} = \dfrac{3}{{11}}\)\(\; \Rightarrow B'C' = \dfrac{{7.11}}{3} = 25,67\,cm\)
\( + )\,\,\dfrac{5}{{A'C'}} = \dfrac{3}{{11}}\)\(\; \Rightarrow A'C' = \dfrac{{5.11}}{3} = 18,33\,cm\)