Kéo con lắc ra khỏi vị trí cân bằng đến vị trí có li độ góc \(\alpha = {30^0}\) rồi buông ra không vận tốc đầu
\( \Rightarrow \) Biên độ góc \({\alpha _0} = {30^0}\)
a) Chu kì con lắc đơn: \(T = 2\pi \sqrt {\dfrac{l}{g}} = 2\pi \sqrt {\dfrac{2}{{9,8}}} = 2,8s\)
b) Ta có công thức tính động năng
\(\begin{array}{l}\left\{ \begin{array}{l}{{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\\{{\rm{W}}_d} = mgl(\cos \alpha - \cos {\alpha _0})\end{array} \right.\\ \Rightarrow v = \sqrt {2gl(\cos \alpha - \cos {\alpha _0})} \\ = \sqrt {2.9,8.2(\cos {0^0} - \cos {{30}^0})} \\ = 2,3(m/s)\end{array}\)
Áp dụng định luật II Niuton:
\(\overrightarrow F + \overrightarrow P = m\overrightarrow a \)
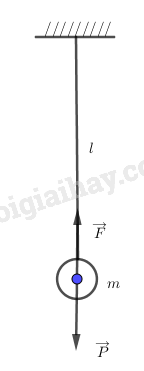
Chiếu theo phương hướng tâm:
\(\begin{array}{l}F - P = m{a_{ht}} = m\dfrac{{{v^2}}}{l}\\ \Leftrightarrow F = P + m\dfrac{{{v^2}}}{l}\\ = P + 2mg(1 - \cos {\alpha _0})\\ = mg + 2mg(1 - \cos {\alpha _0})\\ = mg(3 - 2\cos {\alpha _0})\\ = 0,05.9,8.(3 - 2\cos {30^0}) = 0,64(N)\end{array}\)