Hình 116
Ta có: \(∆ABD\) cân tại \(A\) vì có \(AB=AD.\)
\(∆ACE\) cân tại \(A\) vì \(AC=AE\) (do \(AB=AD,BC=DE\) nên \(AB+BC=AD+DE\) hay \(AC= AE\)).
Hình 117
Ta tính được
\(\widehat{G} = {180^o}- (\widehat{H}+ \widehat{I})\)\(\, = {180^0} - ({70^0} + {40^0}) = {70^0}\)
Do đó \(∆GHI\) cân tại \(I\) vì \(\widehat{G} = \widehat{H}= {70^0}\)
Hình 118
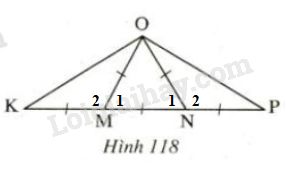
\(∆OMK\) là tam giác cân tại \(M\) vì \(OM= MK\)
\(∆ONP\) là tam giác cân tại \(N\) vì \(ON=NP\)
\(∆OMN\) là tam giác đều vì \(OM = MN = ON\)
Do đó: \(\widehat {{M_1}} = \widehat {{N_1}} = {60^0}\) (1)
\(\widehat {{M_1}} + \widehat {{M_2}} = {180^0}\) (hai góc kề bù) (2)
\(\widehat {{N_1}} + \widehat {{N_2}} = {180^0}\) (hai góc kề bù) (3)
Từ (1), (2) và (3) suy ra: \(\widehat {{M_2}} = \widehat {{N_2}}\)
Xét \(∆OMK\) và \(∆ONP\) có:
+) \(OM = ON\) (gt)
+) \(MK = NP\) (gt)
+) \(\widehat {{M_2}} = \widehat {{N_2}}\) (chứng minh trên)
\(\Rightarrow ∆OMK = ∆ONP\) (c.g.c)
\(\Rightarrow \widehat {MKO} = \widehat {NPO}\) (hai góc tương ứng)
Vậy \(∆OKP\) là tam giác cân tại \(O.\)