Bài 7. Định lí Py-ta-go
Bài Tập và lời giải
Đề bài
Lấy giấy trắng cắt tám tam giác vuông bằng nhau. Trong mỗi tam giác vuông đó, ta gọi độ dài các cạnh góc vuông là \(a\) và \(b\), gọi độ dài cạnh huyền là \(c.\) Cắt hai tấm bìa hình vuông có cạnh bằng \(a+b\).
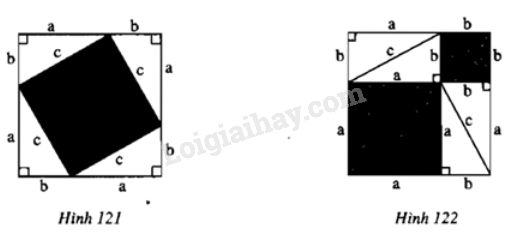
a) Đặt bốn tam giác vuông lên tấm bìa hình vuông như hình 121. Phần bìa không bị che lấp là một hình vuông có cạnh bằng \(c\), tính diện tích phần bìa đó theo \(c\).
b) Đặt bốn tam giác vuông còn lại lên tấm bìa hình vuông thứ hai như hình 122. Phần bìa không bị che lấp gồm hai hình vuông có cạnh là \(a\) và \(b\); tính diện tích phần bìa đó theo \(a\) và \(b\)
c) Từ đó rút ra nhận xét gì về quan hệ giữa \(c^2\) và \(a^2 + b^2 \)?
Đề bài
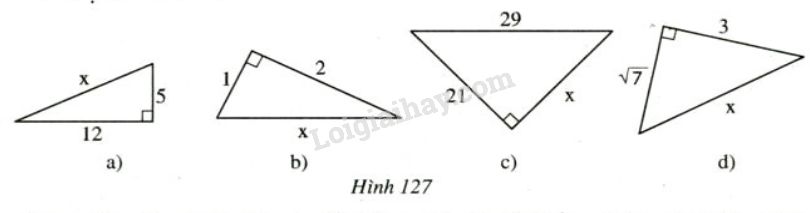
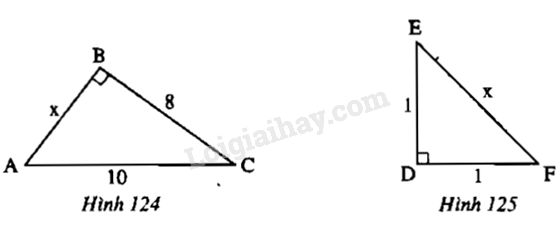
Tìm độ dài \(x\) trên các hình 124, 125
Đề bài
Vẽ tam giác \(ABC\) có \(AB = 3\,cm; AC = 4\,cm; BC = 5\,cm.\) Hãy dùng thước đo góc để xác định số đo của góc \(BAC\).
Đề bài
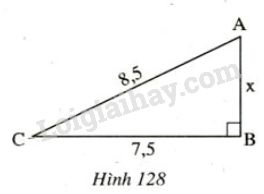
Đoạn lên dốc từ \(C \) đến \(A \) dài \(8,5m\) , độ dài \(CB\) bằng \(7,5m.\)
Tính chiều cao \( AB.\)
Đề bài
Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:
a) \(9cm,15cm,12cm.\)
b) \(5dm,13dm,12dm.\)
c)\( 7m,7m,10m.\)
Đề bài
Cho bài toán "Tam giác \(ABC\) có \(AB = 8, AC=17, BC =15\) có phải là tam giác vuông không?" Bạn Tâm giải thích như sau:
\( AB^2 + AC^2 = 8^2 +17^2 = 64+289\)\(=353\)
\(BC^2=15^2=225\)
Do \(353 ≠ 225\) nên \(AB^2+AC^2 ≠ BC^2\).
Vậy tam giác \(ABC\) không phải là tam giác vuông?
Đề bài
Đố: Trong lúc anh Nam dựng tủ cho đứng thẳng, tủ vướng vào trần nhà không?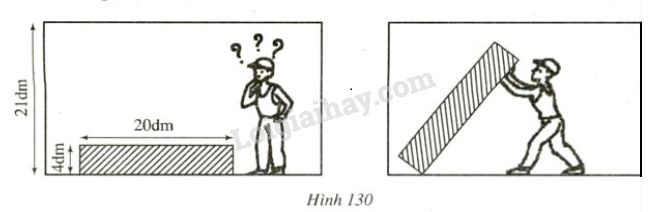
Đề bài
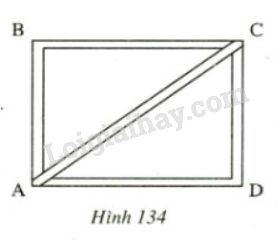
Bạn Tâm muốn đóng cho một nẹp chéo \(AC\) để khung hình chữ nhật \(ABCD\) được vững hơn(h.134). Tính độ dài \( AC\), Biết rằng \(AD=48 cm, CD=36 cm.\)
Đề bài
Cho tam giác nhọn \(ABC\). Kẻ \(AH\) vuông góc với \(BC \) (\(H \) thuộc \( BC\)), cho biết \(AB = 13cm, AH = 12cm, HC = 16 cm\). Tính độ dài \(AC;BC\)
Đề bài
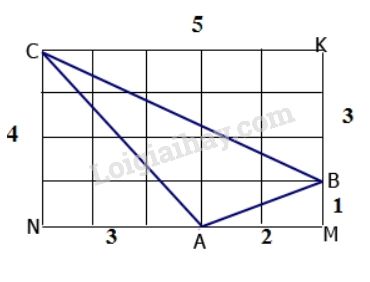
Trên giấy ô vuông (Độ dài cạnh của ô vuông bằng 1), cho tam giác \(ABC \) như hình 135.
Tính độ dài mỗi cạnh của tam giác \(ABC.\)
Đề bài
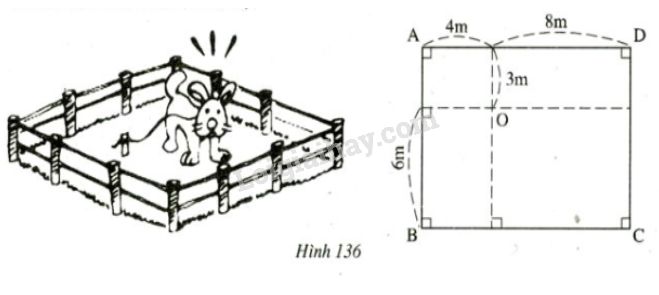
Đố: Người ta buộc con Cún bằng sợi dây có một đầu buộc tại điểm \(O\) làm cho con Cún cách điểm \(O\) nhiều nhất là \(9m\) (h.136). Con cún có thể tới các vị trí \(A,B,C,D\) để canh giữ mảnh vườn hình chữ nhật \(ABCD\) hay không? (Các kích thước như trên hĩnh vẽ).
Đề bài
Bài 1. Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC, biết AB = 20cm, AH = 12cm, AC = 15cm. Tính BC, BH, CH.
Bài 2. Các tam giác cho dưới đây có phải là tam giác vuông không? Hãy chứng minh, nếu là tam giác vuông cho biết vuông tại đỉnh nào?
a) \(AB = 8cm;\,AC = 17cm;\,BC = 15cm.\)
b) \(AB = 25cm;\,AC = 24cm;\,BC = 6cm.\)
Đề bài
Bài 1. Cho tam giác nhọn ABC, kẻ AH vuông góc với BC \(\left( {H \in BC} \right)\), biết \( \Rightarrow AC = \sqrt {400} = 20\,(cm)\) \(AB = 13cm;\,AH = 12cm;\,\)\(HC = 16cm\). Tính AC, BC.
Bài 2. Cho tam giác ABC vuông tại A. Một đường thẳng cắt hai cạnh AB, AC ở D và E. Chứng minh: \(C{D^2} - C{B^2} = E{D^2} - E{B^2}.\)
Đề bài
Cho tam giac ABC cân tại A, kẻ BH vuông góc với AC. Biết AH= 6cm, CH = 4cm. Tính BC.
Đề bài
Cho tam giác ABC vuông ở A có \(\dfrac{{AB}}{ {AC}} = \dfrac{8 }{ {15}}\) và BC = 51cm.
a) Tính AB, AC.
b) Tính diện tích tam giác ABC
Đề bài
Cho góc nhọn xOy, trên Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Từ A và B kẻ AH, BK lần lượt vuông góc với Oy và Ox.
a) Chứng minh \(\Delta OHA = \Delta OKB.\)
b) Gọi I là giao điểm của AH và BK. Chứng minh rằng OI là phân giác của góc \(\widehat {xOy}.\)
Đề bài
Cho tam giác ABC cân tại A, vẽ BD, CE lần lượt vuông góc với AC và AB. Gọi I là giao điểm cả BD và CE.
a) Chứng minh rằng \(\Delta AEI = \Delta ADI.\)
b) Gọi M là trung điểm của BC. Chứng minh ba điểm A, I, M thẳng hàng.
Đề bài
Cho tam giác ABC cân tại A. Kẻ qua B tia Bx vuông góc với AB, qua C kẻ tia Cy vuông góc với AC, gọi I là giao điểm của Bx và Cy.
a) Chứng minh \(\Delta ABI = \Delta ACI.\)
b) Chứng tỏ AI là đường trung trực của đoạn BC.
Đề bài
Cho tam giác ABC cân tại A \(\left( {\widehat A < {{90}^o}} \right)\), các đường trung trực của AB, AC cắt nhau tại O.
a) Chứng minh rằng AO là tia phân giác của góc A.
b) Kẻ đường vuông góc với AB qua B, kẻ đường vuông góc với AC qua C, chúng cắt nhau tại K. Chứng tỏ ba điểm A, O, K thẳng hàng.
Đề bài
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC.
a) Chứng minh \(\Delta AHB = \Delta AHC\)
b) Trên tia đối của tia BC lấy điểm D, trên tia đối của tia Cb lấy điểm E sao cho \(BD = CE\). Chứng minh rằng \(\Delta ADE\) cân.