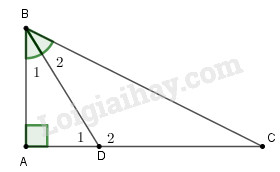
a) Xét tam giác \(BCD\) có \(\widehat {{D_1}}\) là góc ngoài tại đỉnh \(D\) nên \(\widehat {{D_1}} = \widehat {{B_2}} + \widehat C \Rightarrow \widehat {{D_1}} > \widehat {{B_2}}\)
Mà \(\widehat {{B_2}} = \widehat {{B_1}}\) (do \(BD\) là phân giác góc \(B\)) nên \(\widehat {{D_1}} > \widehat {{B_1}}\)
Xét tam giác \(ABD\) có \(\widehat {{D_1}} > \widehat {{B_1}}\) nên \(AB > AD\) (đối diện với góc lớn hơn là cạnh lớn hơn)
b) Hai đường xiên \(BD,BC\) có hai hình chiểu xuống cạnh \(AC\) là \(AD\) và \(AC.\)
Mà \(AD < AC \Rightarrow BD < BC\) (quan hệ giữa hình chiếu và đường xiên)