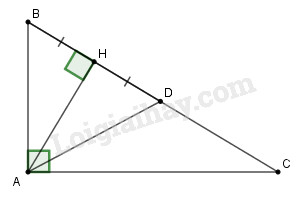
Lấy điểm \(D\) trên tia \(HC\) sao cho \(HB = HD\)
Suy ra \(AH\) là đường trung trực của \(\widehat {BAD}\) (vì \(AH \bot BD;HB = HD\)) nên \(AB = AD\) (tính chất đường trung trực)
Theo giả thiết ta có: \(HC - HB = AB \)\(\Leftrightarrow HC - HD = AB\) (vì \(HB = HD\))
Hay \(CD = AB = AD\) (1)
Ta lại có: \(\Delta DAC\) cân tại \(D\) (do \(DA = DC\)) nên \(\widehat {DCA}\)\( = \widehat {DAC}\)
Mà \(\widehat {ABC} + \widehat {ACB} = 90^\circ \) và \(\widehat {BAD} + \widehat {DAC} = 90^\circ \)
Suy ra \(\widehat {ABC} = \widehat {BAD}\) (cùng phụ với hai góc bằng nhau)
Hay tam giác \(ABD\) cân tại \(D\), suy ra \(DB = DA\) (2)
Từ (1) và (2) ta suy ra \(AB = BD = DC \)\(= \dfrac{{BC}}{2}\) hay \(BC = 2AB.\)