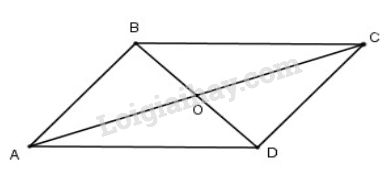
Gọi O là giao điểm của AC và BD. Khi đó O là trung điểm của AC và BD.
Áp dụng định lí về đường trung tuyến:
\(OA^2 =\frac{AD^{2}+AB ^{2}}{2} - \frac{BD^{2}}{4}\)
Thay \(OA = \frac{n}{2}, \, AB = a,\) \(AD = BC = b\) và \(BD = m\) ta được:
\({\left( {{n \over 2}} \right)^2} = {{{b^2} + {a^2}} \over 2} - {{{m^2}} \over 4} \)\(\Rightarrow {n^2} = 2{b^2} + 2{a^2} - {m^2} \)
\(\Rightarrow {m^2} + {n^2} = 2({a^2} + {b^2}).\)