Bài 3. Các hệ thức lượng trong tam giác và giải tam giác

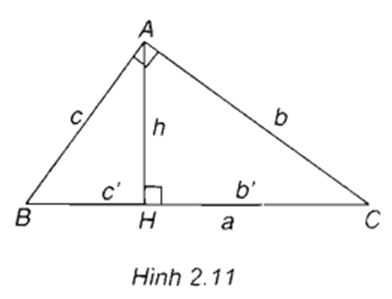
Tam giác ABC vuông tại A có đường cao AH = h và có BC = a, CA = b, AB = c. Gọi BH = c’ và CH = b’(h.2.11). Hãy điền vào các ô trống trong các hệ thức sau đây để được các hệ thức lượng trong tam giác vuông:

a² = b² + (.....)                              h² = b’ x (.....)

b² = a x (.....)                               ah = b x (.....)

c² = a x (.....)

\(\eqalign{
& {1 \over } = {1 \over {{b^2}}} + {1 \over {{c^2}}} \cr 
& \sin B = \cos C = { \over a} \cr 
& \sin C = \cos B = { \over a} \cr 
& \tan B = \cot C = { \over c} \cr 
& \cot B = \tan C = { \over b} \cr} \)

Khi ABC là tam giác vuông, định lý côsin trở thành định lý quen thuộc nào ?

Cho tam giác ABC có a = 7cm, b = 8cm, c = 6cm. Hãy tính độ dài đường trung tuyến m_a của tam giác ABC đã cho.

Cho tam giác ABC vuông ở A nội tiếp trong đường tròn bán kính R và có BC = a, CA = b, AB = c.

Chứng minh hệ thức:  \({a \over {\sin A}} = {b \over {\sin B}} = {c \over {\sin C}} = 2R\)

Cho tam giác đều ABC có cạnh bằng a. Hãy tính bán kính đường tròn ngoại tiếp tam giác đó.

Hãy viết các công thức tính diện tích tam giác theo một cạnh và đường cao tương ứng.

Dựa vào công thức (1) và định lý sin. Hãy chứng minh: \(S = {{abc} \over {4R}}\)

Chứng minh công thức S = pr (h.2.19).

Cho tam giác \(ABC\) vuông tại \(A\), \(\widehat{B}= 58^0\) và cạnh \(a = 72 cm\). Tính \(\widehat{C}\), cạnh \(b\), cạnh \(c\) và đường cao \(h_a\)

Cho tam giác \(ABC\) biết các cạnh \(a = 52, 1cm\); \(b = 85cm\) và \(c = 54cm\). Tính các góc \(\widehat{A}\), \(\widehat{B}\), \(\widehat{C}\).

Cho tam giác \(ABC\) có \(\widehat{A}  = 120^0\) cạnh \(b = 8cm\) và \(c = 5cm\). Tính cạnh \(a\), và góc  \(\widehat{B}\), \(\widehat{C}\) của tam giác đó.

Tính diện tích \(S\) của tam giác có số đo các cạnh lần lượt là \(7, \, \,9\) và \(12\).

Tam giác \(ABC\) có  \(\widehat{A} = 120^0\). Tính cạnh \(BC\) cho biết cạnh \(AC = m\) và \(AB = n\).

Tam giác \(ABC\) có các cạnh \(a = 8cm, \,  b = 10cm, \,  c = 13cm.\)

a) Tam giác đó có góc tù không? 

b) Tính độ dài đường trung tuyến \(MA\) của tam giác \(ABC\) đó.

Tính góc lớn nhất của tam giác \(ABC\) biết:

a) Các cạnh \(a = 3cm, \, b = 4cm,\, c = 6cm.\)

b) Các cạnh \(a = 40cm, \, b = 13cm, \, c = 37cm.\)

Cho tam giác \(ABC\) biết cạnh \(a = 137,5cm; \widehat{B} = 83^0, \, \widehat{C} = 57^0.\) Tính góc \(A,\) cạnh \(b\) và \(c\) của tam giác.

Cho hình bình hành \(ABCD\) có \(AB = a, BC = b ,BD = m\), và \(AC = n\). Chứng minh rằng :

$${m^2} + {n^2} = 2({a^2} + {b^2})$$

Hai chiếc tàu thủy \(P\) và \(Q\) cách nhau \(300m\).Từ \(P\) và \(Q\) thẳng hàng với chân \(A\) của tháp hải đăng \(AB\) ở trên bờ biển người ta nhìn chiều cao \(AB\) của tháp dưới các góc \(\widehat {BPA} = {35^0},\widehat {BQA} = {48^0}.\) Tính chiều cao của tháp.

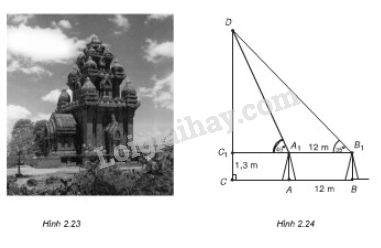
Muốn đo chiều cao của tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm \(A\) và \(B\) trên mặt đất có khoảng cách \(AB = 12m\) cùng thẳng hàng với chân \(C\) của tháp để đặt hai giác kế. Chân của giác kế có chiều cao \(h = 1,3m\). Gọi \(D\) là đỉnh tháp và hai điểm \(A_1, \, B_1\) cùng thẳng  hàng với \(C_1\) thuộc chiều cao \(CD\) của tháp. Người ta đo được \(\widehat {D{A_1}{C_1}} = {49^0}\) và \(\widehat {D{B_1}{C_1}} = {35^0}.\) Tính chiều cao của  \(CD\) của tháp đó.