Bài 1.Ta có: \(\left\{ \matrix{ a \bot c \hfill \cr b \bot c \hfill \cr} \right. \Rightarrow a//b\). Do đó \(x + y = {180^o}\)(cặp góc trong cùng phía).
Lại có \({x \over 5} = {y \over 4} = {{x + y} \over {4 + 5}} = {{{{180}^o}} \over 9} = {20^o}\)
\(\; \Rightarrow x = {100^o}\) và \(y = {80^o}.\)
b) \(\left\{ \matrix{ AH \bot Oy \hfill \cr Oy//At\,(cmt) \hfill \cr} \right. \Rightarrow AH \bot At.\)
Bài 2.
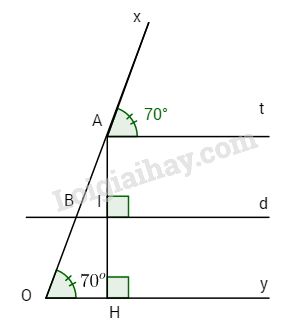
a) Hai góc \(\widehat {xAt}\) và \(\widehat {xOy}\) ở vị trí đồng vị, mà \(\widehat {xAt} = \widehat {xOy} = {70^o}\) nên At // Oy.
c) Ta có: \(\widehat {xAt} + \widehat {tAH} + \widehat {HAO} = {180^o}\)
\(\eqalign{& \Rightarrow \widehat {OAH} = {180^o} - \left( {\widehat {xAt} + \widehat {tAH}} \right) \cr & \Rightarrow \widehat {OAH} = {180^o} - \left( {{{70}^o} + {{90}^o}} \right) \cr & \Rightarrow \widehat {OAH} = {180^o} - {160^o} \cr&\Rightarrow \widehat {OAH} = {20^o} \cr} \)
d) Ta có: \(\left\{ \matrix{ d \bot AH \hfill \cr AH \bot At\,(cmt) \hfill \cr} \right. \Rightarrow d//At.\)
Bài 3.
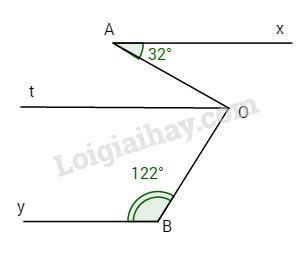
Kẻ qua O tia Ot // Ax (1).Hai góc \(\widehat {OBI}\) và \(\widehat {OAt}\) ở vị trí đồng vị \( \Rightarrow \widehat {OBI} = \widehat {OAt}.\)
Ta có \(\widehat {OAt} = \widehat {xAO} = {32^o}\)(cặp góc so le trong).
Lại có Ax // By (2). Từ (1) và (2) \( \Rightarrow Ot//By\), mà hai góc \(\widehat {tOB}\) và \(\widehat {OBy}\) ở vị trí trong cùng phía nên \(\widehat {tOB} + \widehat {OBy} = {180^o}\)
\(OA \bot OB.\) \( \Rightarrow \widehat {tOB} = {180^o} - \widehat {OBy} \)\(\;= {180^o} - {122^o} = {58^o}\).
Tia Ot nằm giữa hai tia OA và OB, ta có \(\widehat {AOt} + \widehat {tOB} = \widehat {AOB}\)
Hay \(\eqalign{ & \widehat {AOB} = {32^o} + {58^o} \cr & \widehat {AOB} = {90^o}. \cr} \)
Chứng tỏ \(OA \bot OB.\)