Đề số 2 - Đề kiểm tra học kì 2 - Toán lớp 5

Câu 1. Khoanh vào chữ đặt trước đáp số đúng.

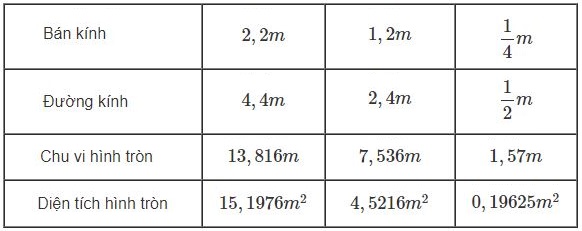
Điểm nào là tâm của hình tròn ?

A. Điểm N

B. Điểm Q

C. Điểm P

D. Điểm M

Câu 2. Khoanh vào chữ đặt trước câu trả lời đúng.

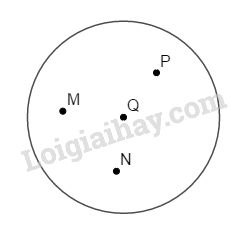
Hình tròn bên có bao nhiêu bán kính ?

A. 2 bán kính

B. 3 bán kính

C. 5 bán kính

D. 6 bán kính.

Câu 3. Đúng ghi Đ, sai ghi S vào ô trống :

Chu vi hình tròn có bán kính 2,7cm là :

Câu 4. Đúng ghi Đ, sai ghi S vào ô trống :

Chu vi hình tròn có đường kính 2,5dm là :

Câu 5. Khoanh vào chữ đặt trước đáp số đúng.

Đường kính một hình tròn là 0,6m. Diện tích hình tròn đó là :

A. 1,884m²                            B. 0,2826m²                         C. 2,826m²

Câu 6. Đúng ghi Đ, sai ghi S vào ô trống :

Bán kính một hình tròn là 0,8m. Diện tích hình tròn đó là :

Câu 7. Tính rồi viết kết quả vào ô trống.

Câu 8. Đường từ nhà Luân đến trường dài 2245,1m ; Luân đi học bằng xe đạp có bán kính xe là 0,325m. Hỏi bánh xe đạp của Luân phải quay bao nhiêu vòng thì tới trường ?

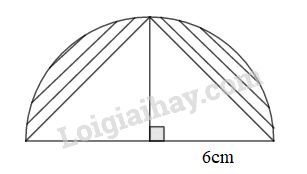
Câu 9. Tính diện tích phần gạch chéo

Câu 1.

Phương pháp:

Quan sát hình vẽ để tìm tâm của hình tròn đã cho.

Cách giải:

Quan sát hình vẽ ta thấy tâm của hình tròn đã cho là điểm Q.

Chọn B.

Câu 2.

Phương pháp:

Quan sát hình vẽ để tìm bán kính của hình tròn đã cho. Bán kính chính là đoạn thẳng nối tâm với một điểm trên đường tròn.

Cách giải:

Hình tròn đã cho có \(6\) bán kính được đánh số như hình vẽ:

Chọn D.

Câu 3.

Phương pháp:

Muốn tính chu vi hình tròn ta lấy \(2\) lần bán kính nhân với số \(3,14\).

Cách giải:

Chu vi hình tròn có bán kính \(2,7cm\) là:

               \(2,7 \times 2 \times 3,14 = 16,956\;(cm)\)

Vậy ta có bảng kết quả như sau: 

Câu 4.

Phương pháp:

 Muốn tính chu vi hình tròn ta lấy đường kính nhân với số \(3,14\).

Cách giải:

Chu vi hình tròn có đường kính \(2,5dm\) là:

               \(2,5 \times 3,14 = 7,85\;(dm)\)

Vậy ta có bảng kết quả như sau: 

Câu 5.

Phương pháp:

- Tính bán kính = đường kính \(:\,2\).

- Muốn tính diện tích của hình tròn ta lấy bán kính nhân với bán kính rồi nhân với số \(3,14\).

Cách giải:

Bán kính hình tròn đó là:

               \(0,6:2=0,3\;(m)\)

Diện tích hình tròn đó là:

               \(0,3 \times 0,3 \times 3,14 = 0,2826\;(m^2)\)

Chọn B.

Câu 6.

Phương pháp:

Muốn tính diện tích của hình tròn ta lấy bán kính nhân với bán kính rồi nhân với số \(3,14\).

Cách giải:

Diện tích hình tròn đó là:

               \(0,8 \times 0,8 \times 3,14 = 2,0096\;(m^2)\)

Vậy ta có bảng kết quả như sau:

Câu 7.

Phương pháp:

- Muốn tính bán kính ta lấy đường kính chia cho \(2\).

- Muốn tính chu vi hình tròn ta lấy đường kính nhân với số \(3,14\) hoặc lấy \(2\) lần bán kính nhân với số \(3,14\).

- Muốn tính diện tích của hình tròn ta lấy bán kính nhân với bán kính rồi nhân với số \(3,14\).

Cách giải:

+) Hình tròn bán kính \(2,2m\)

Đường kính hình tròn đó là:

              \(2,2 \times 2 = 4,4\;(m)\)

Chu vi hình tròn đó là:

              \( 2,2\times 2 \times 3,14  = 13,816\;(m)\)

Diện tích hình tròn đó là:

              \( 2,2\times 2,2 \times 3,14= 15,1976\;(m^2 )\)

+) Hình tròn đường kính \(2,4m\)

Bán kính hình tròn đó là:

              \(2,4 : 2 = 1,2\;(m)\)

Chu vi hình tròn đó là:

              \( 2,4 \times 3,14 = 7,536\;(m)\)

Diện tích hình tròn đó là:

              \(1,2 \times 1,2 \times 3,14 = 4,5216\;(m^2 )\)

+) Hình tròn bán kính \(\dfrac{1}{4}m\)

Đường kính hình tròn đó là:

              \(\dfrac{1}{4} \times 2 = \dfrac{1}{2}\;(m)\)

Chu vi hình tròn đó là:

              \( \dfrac{1}{4} \times 2 \times  3,14 = 1,57\;(m)\)

Diện tích hình tròn đó là:

              \( \dfrac{1}{4} \times \dfrac{1}{4} \times 3,14 = 0,19625\;(m^2 )\)

Ta có bảng kết quả như sau:

Câu 8.

Phương pháp:

Tính chu vi bánh xe ta lần hai lần bán kính nhân với số \(3,14\).

Chu vi bánh xe chính là quãng đường đi được khi bánh xe quay \(1\) vòng.

Để tính số vòng bánh xe phải quay khi Luân đi từ nhà đến trường ta lấy quãng đường từ nhà Luân đến trường chia cho chu vi của bánh xe.

Cách giải:

Chu vi bánh xe là:

              \(0,325 \times 2 \times 3,14 = 2,041\; (m)\)

Số vòng bánh xe phải quay là:

              \(2245,1 : 2,041 = 1100 \) (vòng)

Câu 9. 

Phương pháp:

Diện tích phần gạch chéo bằng diện tích nửa hình tròn bán kính \(6cm\) trừ đi \(2\) lần diện tích tam giác vuông có độ dài hai cạnh góc vuông đều là \(6cm\).

Cách giải:

Diện tích hình tròn bán kính \(6cm\) là:

              \(6 \times 6 \times 3,14= 113,04\; (cm^2) \)

Diện tích nửa hình tròn bán kính \(6cm\) là:

              \( 113,04:2 = 56,52\; (cm^2) \)

Diện tích tam giác vuông có độ dài hai cạnh góc vuông đều là \(6cm\) là

              \(6 \times 6 : 2 = 18\; (cm^2) \) 

Diện tích phần tô đậm là: 

              \(56,52 - 18 \times 2 = 20,52\; (cm^2)\)

                                    Đáp số: \(20,52cm^2\).