Bài 1.
a)\({x^2} + xy - x - y = x\left( {x + y} \right) - \left( {x + y} \right) = \left( {x + y} \right)\left( {x - 1} \right).\)
b)\({a^2} - {b^2} + 8a + 16 = \left( {{a^2} + 8a + 16} \right) - {b^2} = {\left( {a + 4} \right)^2} - {b^2}\)
\( = \left( {a + 4 - b} \right)\left( {a + 4 + b} \right).\)
Bài 2.
a) \(4x\left( {x + 1} \right) + \left( {3 - 2x} \right)\left( {3 + 2x} \right) = 15 \Rightarrow 4{x^2} + 4x + \left( {9 - 4{x^2}} \right) = 15\)
\( \Rightarrow 4{x^2} + 4x + 9 - 4{x^2} = 15 \Rightarrow 4x = 15 - 9 \Rightarrow 4x = 6 \Rightarrow x = {3 \over 2}.\)
b) \(3x\left( {x - 20012} \right) - x + 20012 = 0 \Rightarrow 3x\left( {x - 20012} \right) - \left( {x - 20012} \right) = 0\)
\( \Rightarrow \left( {x - 20012} \right)\left( {3x - 1} \right) = 0 \Rightarrow x - 20012 = 0\) hoặc \(3x - 1 = 0\)
\( \Rightarrow x = 20012\) hoặc \(x = {1 \over 3}.\)
Bài 3.
a) Điều kiện: \(x,y \ne 0;x \ne y.\)
\({1 \over {x\left( {x - y} \right)}} + {1 \over {y\left( {y - x} \right)}} = {1 \over {x\left( {x - y} \right)}} - {1 \over {y\left( {x - y} \right)}} = {{y - x} \over {xy\left( {x - y} \right)}} = - {1 \over {xy}}.\)
b) Điều kiện: \(x \ne \pm 1.\)
\({{x - 3} \over {x + 1}} - {{x + 2} \over {x - 1}} - {{8x} \over {1 - {x^2}}} = {{x - 3} \over {x + 1}} - {{x + 2} \over {x - 1}} + {{8x} \over {{x^2} - 1}}\)
\( = {{\left( {x - 3} \right)\left( {x - 1} \right) - \left( {x + 2} \right)\left( {x + 1} \right) + 8x} \over {{x^2} - 1}}\)
\( = {{{x^2} - x - 3x + 3 - \left( {{x^2} + x + 2x + 2} \right) + 8x} \over {{x^2} - 1}}\)
\( = {{{x^2} - x - 3x + 3 - {x^2} - x - 2x - 2 + 8x} \over {{x^2} - 1}} = {{x + 2} \over {\left( {x - 1} \right)\left( {x + 1} \right)}} = {1 \over {x - 1}}.\)
Bài 4.
Ta có \({x^4} + {y^4} = {\left( {{x^2} + {y^2}} \right)^2} - 2{x^2}{y^2} = {18^2} - {2.5^2} = 274.\)
Bài 5.
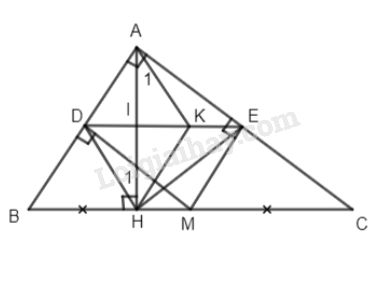
a) Ta có tứ giác ADME là hình chữ nhật (có ba góc vuông).
b) + Ta có \(ME\parallel AB\) (cùng vuông góc AC)
M là trung điểm của BC (gt)
\( \Rightarrow E\) là trung điểm của AC.
+ Ta có E là trung điểm của AC (cmt)
Chứng minh tương tự ta có D là trung điểm của AB
Do đó DE là đường trung bình của \(\Delta ABC\)
\( \Rightarrow DE\parallel BC\) và \(DE = {{BC} \over 2}\) hay \(DE\parallel MC\) và DE = MC
\( \Rightarrow \) Tứ giác CMDE là hình bình hành.
c) Ta có \(DE\parallel HM(cmt) \Rightarrow MHDE\) là hình thang (1)
Lại có \(HE = {{AC} \over 2}\) (tính chất đường trung tuyến của tam giác vuông AHC)
\(DM = {{AC} \over 2}\) (DM là đường trung bình của \(\Delta ABC) \Rightarrow HE = DM\) (2)
Từ (1) và (2) \( \Rightarrow MHDE\) là hình thang cân.
d)Gọi I là giao điểm của AH và DE. Xét \(\Delta AHB\) có D là trung điểm của AB, \(DI\parallel BH\left( {cmt} \right) \Rightarrow I\) là trung điểm của AH.
Xét \(\Delta DIH\) và \(\Delta KIA\) có IH = IA (cmt), \(\widehat {DIH} = \widehat {AIK}\) (đối đỉnh), \(\widehat {{H_1}} = \widehat {{A_1}}\) (so le trong)
\( \Rightarrow \Delta DIH = \Delta KIA(g.c.g) \Rightarrow ID = IK\)
Tứ giác ADHK có ID = IK, IA = IH (cmt) \) \Rightarrow DHK\) là hình bình hành
\( \Rightarrow HK\parallel DA\) mà \(DA \bot AC \Rightarrow HK \bot AC.\)