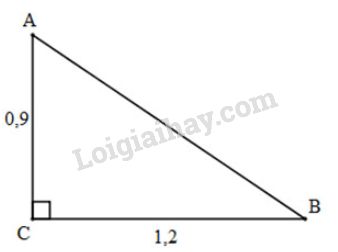
Xét \(\Delta{ABC}\) vuông tại \(C\), áp dụng định lí Pytago, ta có:
\(AB^2=CB^2+AC^2\)
\(\Leftrightarrow AB^2=0,9^2+1,2^2\)
\(\Leftrightarrow AB^2=0,81+1,44=2,25\)
\(\Leftrightarrow AB=\sqrt{2,25}=1,5\)
Vì \(\Delta{ABC}\) vuông tại \(C\) nên góc \(B\) và \(A\) là hai góc phụ nhau. Do vậy, ta có:
\(\sin A=\cos B=\dfrac{BC}{AB}=\dfrac{1,2}{1,5}=\dfrac{4}{5}\)
\(\cos A=\sin B=\dfrac{AC}{AB} =\dfrac{0,9}{1,5}=\dfrac{3}{5}\)
\(\tan A=\cot B=\dfrac{BC}{AC}=\dfrac{1,2}{0,9}=\dfrac{4}{3}\)
\(\cot A=\tan B=\dfrac{AC}{BC}=\dfrac{0,9}{1,2}=\dfrac{3}{4}\)
Nhận xét: Với hai góc phụ nhau, ta có sin góc này bằng cosin góc kia, tan góc này bằng cotan góc kia!