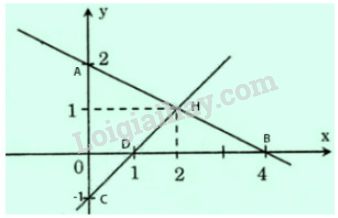
* Ta có: \(x + 2y = 4 \Rightarrow 2y=-x+4 \Rightarrow y=-\dfrac{1}{2}x+2\).
+ Cho \(x = 0 \Rightarrow y = 2\) ta được \(A(0;2)\).
+ Cho \(y = 0 \Rightarrow x = 4\) ta được \(B(4;0)\).
Đường thẳng cần vẽ là đường thẳng đi qua \(A,\ B\).
 ư
ư
* Ta có: \(x - y = 1 \Rightarrow y=x-1\).
+ Cho \(x = 0 \Rightarrow y = - 1\) ta được \(C(0; -1)\).
+ Cho \(y = 0 \Rightarrow x = 1\) ta được \(D(1; 0)\).
Đường thẳng cần vẽ là đường thẳng đi qua \(C,\ D\).
* Tìm giao điểm:
Hoành độ giao điểm là nghiệm của phương trình:
\(-\dfrac{1}{2}x+2=x-1 \)
\(\Leftrightarrow -\dfrac{1}{2}x-x=-1-2\)
\(\Leftrightarrow -\dfrac{3}{2}x=-3 \)
\(\Leftrightarrow x=2\)
\(\Rightarrow y=2-1=1\)
Vậy tọa độ giao điểm của hai đường thẳng trên là \((2; 1)\). Tọa độ của nó là nghiệm của cả hai phương trình đã cho.