a) Hoành độ giao điểm của đường cong đã cho và trục hoành là nghiệm của phương trình:
\(\left( {x + 1} \right)\left( {{x^2} + 2mx + m + 2} \right) = 0 \Leftrightarrow \left[ \matrix{ x = - 1 \hfill \cr {x^2} + 2mx + m + 2 = 0\,\,\left( 1 \right) \hfill \cr} \right.\)
đồ thị của hàm số đã cho cắt trục hoành tại \(3\) điểm phân biệt khi và chỉ khia phương trình (1) có hai nghiệm phân biệt khác -1, tức là:
\(\eqalign{
& \left\{ \matrix{
\Delta ' > 0 \hfill \cr
f\left( { - 1} \right) \ne 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{m^2}-m - 2 > 0 \hfill \cr
- m + 3 \ne 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
\left[ \matrix{
m < - 1 \hfill \cr
m > 2 \hfill \cr} \right. \hfill \cr
m \ne 3 \hfill \cr} \right. \cr
& \Leftrightarrow m \in \left( { - \infty ; - 1} \right) \cup \left( {2;3} \right) \cup \left( {3; + \infty } \right). \cr} \)
b) Với \(m =-1\) ta có \(y = \left( {x + 1} \right)\left( {{x^2} - 2x + 1} \right) = {x^3} - {x^2} - x + 1\)
TXĐ: \(D =\mathbb R\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \cr
& y' = 3{x^2} - 2x - 1;\,y' = 0 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = - {1 \over 3} \hfill \cr} \right.;\,\,y\left( 1 \right) = 0;\,\,y\left( { - {1 \over 3}} \right) = {{32} \over {27}} \cr} \)
Bảng biến thiên:
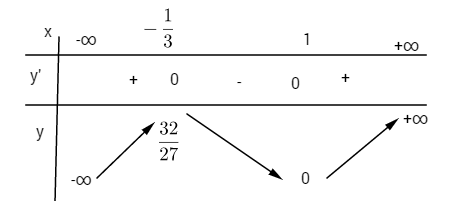
\(y'' = 6x - 2;\,y'' = 0 \Leftrightarrow x = {1 \over 3};\,y\left( {{1 \over 3}} \right) = {{16} \over {27}}\)
Xét dấu \(y”\)
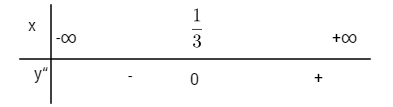
Điểm uốn \(I\left( {{1 \over 3};{{16} \over {27}}} \right)\)
Điểm đồ thị đi qua:
\(x = 0 \Rightarrow y = 1\)
\(x = 2 \Rightarrow y = 3\)
\(x = -1 \Rightarrow y = 0\)
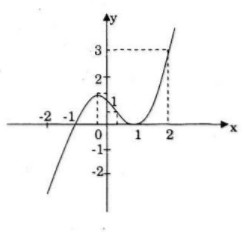
Đồ thị: Đồ thị nhận điểm uốn \(I\) làm tâm đối xứng.