Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Bài 17. Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

a) \(f\left( x \right) = {x^2} + 2x - 5\) trên đoạn \(\left[ { - 2;3} \right]\);

b) \(f\left( x \right) = {{{x^3}} \over 3} + 2{x^2} + 3x - 4\) trên đoạn \(\left[ { - 4;0} \right]\);

c) \(f\left( x \right) = x + {1 \over x}\) trên đoạn \(\left( {0; + \infty } \right)\);

d) \(f\left( x \right) =  - {x^2} + 2x + 4\) trên đoạn \(\left[ {2;4} \right]\);

e) \(f\left( x \right) = {{2{x^2} + 5x + 4} \over {x + 2}}\) trên đoạn \(\left[ {0;1} \right]\);

f) \(f\left( x \right) = x - {1 \over x}\) trên đoạn \(\left( {0;2} \right]\);

Bài 18. Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

a) \(y = 2{\sin ^2}x + 2\sin x - 1\)

b) \(y = {\cos ^2}2x - \sin x\cos x + 4\)

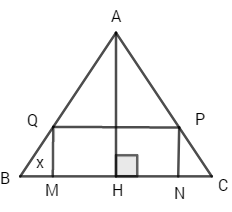
Bài 19. Cho một tam giác đều \(ABC\) cạnh \(a\). Người ta dựng một hình chữ nhật \(MNPQ\) có cạnh \(MN\) nằm trên cạnh \(BC\), hai đỉnh \(P\) và \(Q\) theo thứ tự nằm trên hai cạnh \(AC\) và \(AB\) của tam giác. Xác định vị trí của điểm \(M\) sao cho hình chữ nhật có diện tích lớn nhất và tìm giá trị lớn nhất đó.

Bài 20. Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có \(n\) con cá thì trung bình mỗi con cá sau một vụ cân nặng: \(P(n)=480 – 20n^2\).

Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất.

Bài 21. Tìm cực trị của các hàm số sau:

a) \(f\left( x \right) = {x \over {{x^2} + 1}};\)                    b) \(f\left( x \right) = {{{x^3}} \over {x + 1}};\)

c) \(f\left( x \right) = \sqrt {5 - {x^2}} ;\)              d) \(f\left( x \right) = x + \sqrt {{x^2} - 1} \).

Bài 24. Cho parabol \((P): y = x^2\) và điểm \(A (-3;0)\). Xác định điểm \(M\) thuộc parabol \((P)\) sao cho khoảng cách \(AM\) là ngắn nhất và tìm khoảng cách ngắn nhất đó.

Bài 25. Một con cá hồi bơi ngược dòng để vượt một khoảng cách là \(300km\). Vận tốc dòng nước là \(6 km/h\). Nếu vận tốc bơi của con cá khi nước đứng yên là \(v (km/h)\) thì năng lượng tiêu hao của con cá trong \(t\) giờ được cho bởi công thức \(E\left( v \right) = c{v^3}t\), trong đó \(c\) là một hằng số, \(E\) được tính bằng jun. Tìm vận tốc bơi của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất.

Bài 26. Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là

\(f\left( t \right) = 45{t^2} - {t^3},t = 0,1,2,...,25\)

Nếu coi \(f\) là hàm số xác định trên đoạn \(\left[ {0;25} \right]\) thì \(f'\left( t \right)\) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm \(t\).

a) Tính tốc độ truyền bệnh vào ngày thứ \(5\);

b) Xác định ngày mà tốc độ truyền bệnh là lớn nhất và tính tốc độ đó;

c) Xác định các ngày mà tốc độ truyền bệnh lớn hơn \(600\);

d) Xét chiều biến thiên của hàm số \(f\) trên đoạn \(\left[ {0;25} \right]\).

Bài 27. Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

a) \(f\left( x \right) = \sqrt {3 - 2x} \) trên đoạn \(\left[ { - 3;1} \right]\);

b) \(f\left( x \right) = x + \sqrt {4 - {x^2}} \)

c) \(f\left( x \right) = {\sin ^4}x + {\cos ^2}x + 2;\) 

d) \(f\left( x \right) = x - \sin 2x\) trên đoan \(\left[ { - {\pi  \over 2};\pi } \right]\).

Bài 28. Trong các hình chữ nhật có chu vi là \(40cm\), hãy xác định hình chữ nhật có diện tích lớn nhất.