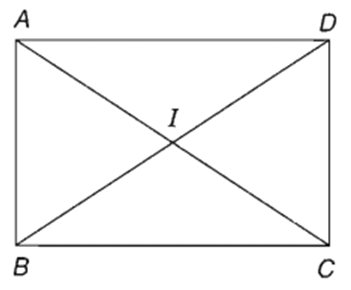
Xét ΔABD vuông tại A có:
\(BD = \sqrt {A{B^2} + A{D^2}} = 2\)
Do ABCD là hình chữ nhật tâm I nên:
\(\eqalign{
& AI = IC = ID = {1 \over 2}BD = 1 \cr
& ICD:\,ID = IC = DC = 1 \cr
& \Rightarrow ICD\,\,deu\,\, \Rightarrow \widehat {DIC} = \widehat {IDC} = {60^0} \cr} \)
Ta có:
\(\widehat {IDC} + \widehat {AID} = {180^0} \Rightarrow \widehat {AID} = {180^0} - {60^0} = {120^0}\)