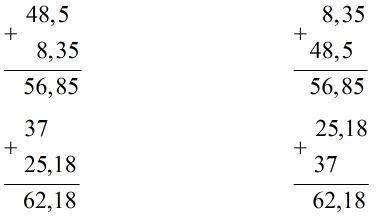Đề số 20 - Đề kiểm tra học kì 1 - Toán lớp 5

Câu 1. Khoanh vào chữ đặt trước câu trả lời đúng:

\(5,235 km +365m = \;?\)

A. 888,5m                               B. 560m

C. 8,885km                             D. 5,6km

Câu 2. Đúng ghi Đ, sai ghi S:

a) \(124,15 + 9,5 + 18,85 = \)

A. 1435 ☐                                B. 143,85  ☐

C. 15,25 ☐                               D. 152,5 ☐

b) \(130,5 + 9,8 + 7,5 + 1,2 = \)

A. 248 ☐                                  B. 14,8 ☐

C. 149 ☐                                  D. 14,90  ☐

Câu 3. Khoanh vào chữ đặt trước câu trả lời đúng:

2,175 tấn + 1912 kg + 20,25 tạ = ..... yến.

Số thích hợp điền vào chỗ chấm là:

A. 6,112                                      B. 61,12

C. 611,2                                      D. 6112

Câu 4. Đúng ghi Đ, sai ghi S:

a) \(48,5 + 8,35 = 132\)  ☐

b) \(8,35 + 48,5 = 56,85\)  ☐

c) \(37 + 25,18 = 62,18\)  ☐

d) \(25,18 + 37 = 25,55\)  ☐

Câu 5. Khoanh vào chữ đặt trước câu trả lời đúng:

Một cửa hàng bán trong 2 ngày đầu được 2,383 tấn gạo, bán trong 3 ngày sau được \(3\dfrac{{67}}{{1000}}\) tấn gạo.

Hỏi trung bình mỗi ngày bán được bao nhiêu tạ gạo ?

A. 105 tạ                               B. 10,5 tạ

C. 10,9 tạ                              D. 109 tạ

Câu 6. Tính bằng cách thuận tiện nhất:

\(0,37 + 5,684 + 3,2 + 0,63 + 5,8 + 4,316\)

Câu 7. Hãy so sánh A và B biết:

\(A = \overline {a,53}  + \overline {4,b6}  + \overline {2,9c} \)

\(B = \overline {a,bd}  + \overline {8,3c}  - \overline {0,8d} \)

Câu 8. Cho ba chữ số \(4;\;5; \;6.\)

a) Hãy viết tất cả các số thập phân có 3 chữ số khác nhau.

b) Tính tổng các số viết được ở câu a) bằng cách thuận tiện nhất.

Câu 1. 

Phương pháp:

Viết \(365m\) thành số đo có đơn vị đo là \(km\) sau đó thực hiện phép cộng hai phân số như thông thường.

Cách giải:

Ta có: \(365m=\dfrac{365}{1000}km=0,365km\).

Do đó: \(5,235 km +365m\) \( =5,235km+0,365km\)\(=5,600km=5,6km\).

Chọn D.

Câu 2.

Phương pháp:

- Cách 1: Biểu thức chỉ có phép cộng thì ta thực hiện lần lượt từ trái sang phải.

- Cách 2: Áp dụng tính chất giao hoán và kết hợp của phép cộng để nhóm các số có tổng là số tự nhiên lại với nhau.

Cách giải:

a) \(124,15 + 9,5 + 18,85 \) \(=(124,15 +18,85) + 9,5 \) \(=143 + 9,5=152,5\)

Ta có kết quả như sau:    A. S;           B. S;           C. S;          D. Đ.

b) \(130,5 + 9,8 + 7,5 + 1,2  \) \(=(130,5+7,5) + (9,8+1,2)\) \(=138 + 11 = 149\)

Ta có kết quả như sau:    A. S;           B. S;           C. Đ;          D. S.

Câu 3. 

Phương pháp:

Đổi các số đo khối lượng về cùng đơn vị đo là yến, sau đó thực hiện phép cộng các số thập phân như thông thường.

Cách giải:

2,175 tấn + 1912 kg + 20,25 tạ

= 217,5 yến + 191,2 yến + 202,5 yến

= 217,5 yến  + 202,5 yến + 191,2 yến

= 420 yến + 191,2 yến 

= 611,2 yến

Chọn C.

Câu 4.

Phương pháp:

 Muốn cộng hai số thập phân ta làm như sau:

- Viết số hạng này dưới số hạng kia làm sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.

- Cộng như cộng các số tự nhiên.

- Viết dấu phẩy ở tổng thẳng cột với các dấu phẩy của các số hạng.

Cách giải:

Ta đặt tính và thực hiện tính như sau:

Ta có kết quả như sau:

a) S;               b) Đ;            c) Đ;         d)  S.

Câu 5. 

Phương pháp:

- Đổi \(3\dfrac{{67}}{{1000}}\) tấn \(=3,067\) tấn.

- Tính tổng số ngày bán hàng : \(2 + 3 =5\) ngày

- Tính tổng số tấn thóc bán được trong \(5\) ngày, sau đó đổi sang đơn vị đo thích hợp.

- Tính số tạ gạo trung bình mỗi ngày bán được ta lấy tổng số gạo bán được trong \(5\) ngày chia cho \(5\).

Cách giải:

Đổi \(3\dfrac{{67}}{{1000}}\) tấn \(=3,067\) tấn.

Cửa hàng đã bán gạo trong số ngày là:

                  \(2+3 = 5\) (ngày)

Trong \(5\) ngày cửa hàng đã bán được số tấn gạo là:

                  \(2,383+3,067=5,45\) (tấn)

                  \(5,45\) tấn \(=545\) yến

Trung bình mỗi ngày cửa hàng bán đước số tạ gạo là:

                  \(545:5 =109 \) (yến)

                   \(109\) yến \(=10,9\) tạ.

                                     Đáp số: \(10,9\) tạ

Chọn C.         

Câu 6. 

Phương pháp:

Áp dụng tính chất giao hoán và kết hợp của phép cộng để nhóm các số có tổng là số tự nhiên lại với nhau.

Cách giải:

\(0,37 + 5,684 + 3,2 + 0,63 + 5,8 \)\(+ 4,316\)

\( = \left( {0,37 + 0,63} \right) + \left( {5,684 + 4,316} \right)\)\( + \left( {3,2 + 5,8} \right)\)

\( = 1 + 10 + 9 = 20.\)

Câu 7. 

Phương pháp:

Tách các số thập phân đã cho thành tổng các số thập phân, sau đó nhóm các số thích hợp lại với nhau rồi so sánh kết quả. 

Cách giải:

\(A = \overline {a,53}  + \overline {4,b6}  + \overline {2,9c} \)

\( = a + 0,53 + 4,06 + \overline {0,b}  + 2,90 \) \(+ \;\overline {0,0c} \)

\( = \left( {a + \overline {0,b}  + \overline {0,0c} } \right) \) \(+ \left( {0,53 + 4,06 + 2,90} \right)\)

\( = \overline {a,bc}  + 7,49.\)

\(B = \overline {a,bd}  + \overline {8,3c}  - \overline {0,8d} \)

\( = \overline {a,b}  + \overline {0,0d}  + 8,3 + \overline {0,0c}  \) \(- \left(  0,8 + \overline {0,0d} \right)\)

\( = \overline {a,b}  + \overline {0,0d}  + 8,3 + \overline {0,0c}  - 0,8 \)\(- \overline {0,0d} \)

\(=\left( {\overline {a,b}  + \overline {0,0d}  + \overline {0,0c}  - \overline {0,0d} } \right) \)\(+ \left( {8,3 - 0,8} \right)\)

\( = \overline {a,bc}  + 7,5.\)

Ta có: \(\overline {a,bc}  = \overline {a,bc} \) và \(7,49 < 7,5\).

Do đó: \(\overline {a,bc}  + 7,49 < \overline {a,bc}  + 7,5\)

Vậy \(A < B\).

Câu 8. 

Phương pháp:

Các số thập phân có 3 chữ số khác nhau được viết từ ba chữ số \(4;\;5; \;6\) sẽ gồm các số thập phân mà phần thập phân có một chữ số hoặc phần thập phân có hai chữ số.

Cách giải:

a) Các số thập phân có phần thập phân có một chữ số: \(45,6\,; \;46,5\,; \; 54,6\,; \; 56,4\,; \; 64,5\,; \; 65,4.\)

Các số thập phân có phần thập phân có hai chữ số: \(4,56 \,; \;4,65\,; \; 5,46 \,; \; 5,64 \,; \; 6,45 \,; \; 6,54 .\)

b) Nhận xét: Trong tất cả các số thập phân lập được ở câu a ta thấy các chữ số \(4;\;5; \;6\) đều đứng ở hàng chục \(2\) lần, hàng đơn vị \(4\) lần, hàng phần mười \(4\) lần, hàng trăm \(2\) lần.

Tổng của \(12\) số đó là:

\(10 \times 2 \times \left( {4 + 5 + 6} \right) + 1 \times 4\)\( \times \left( {4 + 5 + 6} \right) + \dfrac{1}{{10}} \times 4 \times \left( {4 + 5 + 6} \right)\)\( + \dfrac{1}{{100}} \times 2 \times \left( {4 + 5 + 6} \right)\)

\(=20 \times 15 + 4 \times 15 + \dfrac{4}{{10}}\times 15\)\( + \dfrac{2}{{100}} \times 15\)

\( = 300 + 60 + 6 +\dfrac{30}{{100}} \)

\( = 300 + 60 + 6 + 0,3 \)

\(= 366,3.\)