Đề số 30 - Đề kiểm tra học kì 1 - Toán lớp 5

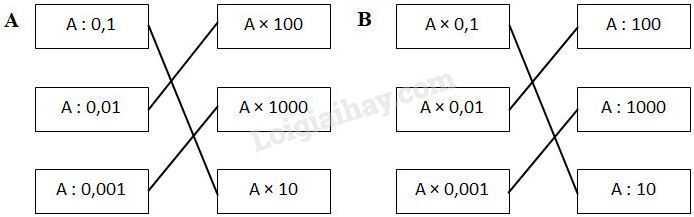
Câu 1. Nối hai phép tính có kết quả bằng nhau:

Câu 2. Đúng ghi Đ, sai ghi S:

a) \(2,08:0,05 < 2,08 \times 20\)  ☐

b) \(2,08:0,05 = 2,08 \times 20\)  ☐

c) \(2,08:0,05 > 2,08 \times 20\)  ☐

Câu 3. Nối hai phép tính có kết quả bằng nhau:

Câu 4. Đúng ghi Đ, sai ghi S:

a) \(5\dfrac{3}{4} = 5,34\)  ☐

b) \(5\dfrac{3}{4} = 5,75\)  ☐

c) \(2\dfrac{1}{{25}} = 2,4\)  ☐

d) \(2\dfrac{1}{{25}} = 2,04\)  ☐

Câu 5. Khoanh vào chữ đặt trước câu trả lời đúng:

Điền dấu \(\left( { > , = , < } \right)\) vào chỗ chấm

\(36:0,125 - 24 \times 0,25 + 12:0,5\) ....... \(36 \times 8 - 24:4 + 12 \times 2\)

A. \(36:0,125 - 24 \times 0,25 + 12:0,5\) \(>\) \(36 \times 8 - 24:4 + 12 \times 2\)

B. \(36:0,125 - 24 \times 0,25 + 12:0,5\) \(< 36\) \(\times 8 - 24:4 + 12 \times 2\)

C. \(36:0,125 - 24 \times 0,25 + 12:0,5\) \(=\) \(36 \times 8 - 24:4 + 12 \times 2\)

Câu 6. Tìm \(x\):

a) \(x \times 18:4 = 72 \times 0,25\)

b) \(x \times 0,125 = \dfrac{{3,6 + 2,8}}{8}\)

Câu 7. Tính bằng cách thuận tiện nhất

\(\left( {792,36 \times 0,75 + 792,36:4} \right)\) \(:\) \(\left( {7,2:0,1:10} \right)\)

Câu 8. Một tàu nhanh đi từ A đến B dài 278,9km, mỗi giờ đi được 54km. Một tàu chợ đi từ C đến B dài 180,5km, mỗi giờ đi được 30km. Hai tàu xuất phát cùng một lúc. Hỏi sau bao lâu hai tàu cùng cách B một khoảng cách bằng nhau?

Câu 1. 

Phương pháp:

Viết số thập phân dưới dạng phân số rồi viết phép chia hai số dưới dạng phép nhân hai số.

Cách giải:

Ta có:

\(A: 0,1 = A: \dfrac{1}{10}= A \times 10\);   

\(A: 0,01 = A: \dfrac{1}{100}= A \times 100\); 

\(A: 0,001 = A: \dfrac{1}{1000}= A \times 1000\); 

\(A \times 0,1 = A \times \dfrac{1}{10}= A :10\); 

\(A \times 0,01 = A \times \dfrac{1}{100}= A :100\);

\(A \times 0,001 = A \times \dfrac{1}{1000}= A :1000\).

Vậy ta có kết quả như sau:

Câu 2. 

Phương pháp:

Tính giá trị hai biểu thức rồi so sánh kết quả với nhau.

Cách giải:

Ta có: \(2,08:0,05 =41,6 \)  ;          \( 2,08 \times 20=41,6\).

Mà:    \(41,6 = 41,6\).

Vậy:   \(2,08:0,05 = 2,08 \times 20\)

Ta có kết quả như sau:     a) S;            b) Đ;           c) S.

Câu 3.

Phương pháp:

Tính giá trị các phép tính rồi so sánh các kết quả với nhau.

Cách giải:

Dãy A: 

\(0,18 :0,2 = 0,9\) ;                           \(0,18 \times 2 = 0,36\) ;

\(0,18 :0,5 = 0,36\) ;                         \(0,18 \times 4 = 0,72\) ;

\(0,18 :0,25 = 0,72\) ;                       \(0,18 \times 5 = 0,9\) ;

Dãy B:

\(0,24 \times 0,2 = 0,048\)                  \(0,24 : 2 = 0,12\) ;

\(0,24 \times 0,5 = 0,12\)                    \(0,24 : 4 = 0,06\) ;

\(0,24 \times 0,25 = 0,06\)                  \(0,24 : 5 = 0,048\).

Vậy ta có kết quả như sau:

Câu 4. 

Phương pháp:

Viết phần phân số của hỗn số dưới dạng phân số thập phân, sau đó viết hỗn số dưới dạng số thập phân.

Cách giải:

+) \(5\dfrac{3}{4} = 5\dfrac{75}{100}= 5,75\) ;

+) \(2\dfrac{1}{{25}} = 2\dfrac{4}{{100}} =2,04\) .

Vậy ta có kết quả như sau:      a) S;          b) Đ;          c) S;         d) Đ.

Câu 5. 

Phương pháp:

Viết số thập phân dưới dạng phân số rồi viết phép chia hai số dưới dạng phép nhân hai số.

Cách giải:

\(36:0,125 - 24 \times 0,25 + 12:0,5\)

\(=36:\dfrac{1}{8} - 24 \times \dfrac{1}{4} + 12:\dfrac{1}{2}\)

\(=36 \times 8 - 24:4 + 12 \times 2\)

Chọn C

Câu 6.

Phương pháp:

- Tính giá trị vế phải trước.

- Áp dụng quy tắc: Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.

Cách giải:

a) \(x \times 18:4 = 72 \times 0,25\)

    \(x \times 18 :4 = 18\)

    \(x \times 18 = 18 \times 4\) 

    \(x \times 18 = 72\)

    \(x = 72:18 \)

    \(x= 4\)

b) \(x \times 0,125 = \dfrac{{3,6 + 2,8}}{8}\)

    \(x \times 0,125 = \dfrac{{6,4}}{8}\)

    \(x \times 0,125 = 0,8\)

    \(x = 0,8 : 0,125\)

    \(x = 6,4\)

Câu 7.

Phương pháp:

- Áp dụng tính chất nhân một số với một tổng:   \(a\times (b+c) = a \times b + a\times c\).

- Khi chia một số thập phân cho \(0,1\) ta chỉ việc chuyển dấu phẩy của số đó sang bên phải \(1\) chữ số.

Cách giải:

\(\left( {792,36 \times 0,75 + 792,36:4} \right)\) \(:\) \(\left( {7,2:0,1:10} \right)\)

\( = \left( {792,36 \times 0,75 + 792,36 \times 0,25} \right)\) \(:\) \(\left( {7,2:0,1:10} \right)\)

\( = 729,36 \times \left( {0,75 + 0,25} \right):\) \(72: 10\)

\( = 729,36 \times 1:7,2 \)

\( = 729,36 :7,2 \)

\(= 110,05\)

Câu 8. 

Phương pháp:

Hai tàu đã cho chuyển động cùng chiều về phía B và xuất phát cùng lúc. Lúc hai tàu cùng cách B một khoảng cách bằng nhau thì lúc đó hai tàu gặp nhau tại một địa điểm D nào đó (D nằm giữa A và B). Để giải bài này ta có thể làm như sau:

- Tìm hiệu độ dài quãng đường từ A đến B và quãng đường từ C đến B.

- Tìm số ki-lô-mét tàu nhanh đi nhiều hơn tàu chợ trong \(1\) giờ.

- Tìm thời gian để hai tàu cùng cách B một khoảng cách bằng nhau (tức thời gian đi để hai tàu gặp nhau kể từ lúc xuất phát) ta lấy hiệu độ dài quãng đường từ A đến B và quãng đường từ C đến B chia cho số ki-lô-mét tàu nhanh đi nhiều hơn tàu chợ trong \(1\) giờ.

Cách giải:

Quãng đường từ A đến B dài hơn quãng đường từ C đến B một đoạn là:

                 \(278,9 - 180,5 = 98,4\;(km)\)

Trong một giờ tàu nhanh đi hơn tàu chợ số ki-lô-mét là:

                  \(54 - 30 = 24\;(km)\)

Hai tàu cùng cách B một khoảng cách bằng nhau sau số giờ kể từ khi xuất phát là:

                   \(98,4:24 = 4,1\) (giờ)

                   \(4,1\) giờ \(= 4\) giờ \(6\) phút

                                             Đáp số: \(4\) giờ \(6\) phút.