Đề số 8 - Đề kiểm tra học kì 1 - Toán lớp 5

Câu 1. Khoanh vào chữ đặt trước câu trả lời đúng:

Tổng của hai số là số lớn nhất có hai chữ số. Tìm hai số đó biết nếu viết thêm một chữ số 0 vào bên phải số bé thì được số lớn.

A. 10 và 90

B. 9 và 99

C. 9 và 90.

Câu 2. Khoanh vào chữ đặt trước câu trả lời đúng:

Một mảnh đất hình chữ nhật có chiều rộng bằng \(\dfrac{2}{5}\) chiều dài. Nếu chiều rộng tăng thêm 9m, chiều dài bớt đi 9m thì mảnh đất trở thành hình vuông.

Tính diện tích mảnh đất đó.

A. 300m²            B. 360m²           C. 420m²

Câu 3. Đúng ghi Đ, sai ghi S:

Một người đi xe máy trong 16 phút được 9km 600m. Hỏi với mức đi như thế trong \(5\dfrac{1}{3}\) giờ thì người đó đi được bao nhiêu ki-lô-mét?

a) 108km            b) 150km           c) 192km

Câu 4. Khoanh vào chữ đặt trước câu trả lời đúng:

18 người làm xong một đoạn đường mất 5 ngày. Hỏi 30 người làm xong đoạn đường đó trong bao nhiêu ngày? (Biết sức làm việc của mỗi người là như nhau).

A. 2 ngày           B. 3 ngày            C. 4 ngày

Câu 5. Tổng số tuổi hiện nay của hai mẹ con là 36 tuổi. Tuổi con bằng \(\dfrac{2}{7}\) tuổi mẹ. Hỏi:

a) Hiện nay mỗi người bao nhiêu tuổi?

b) Mấy năm sau tuổi mẹ gấp 3 lần tuổi con?

Câu 6. 6 người thợ trong 4 giờ quét vôi trên tường được 120m². Hỏi 8 người thợ quét vôi trong mấy giờ thì được 200m². Biết năng suất làm việc của mỗi người như nhau.

Câu 1. 

Phương pháp:

- Tìm tổng của hai số: số lớn nhất có hai chữ số là \(99\).

- Viết thêm một chữ số  \(0\) vào bên phải số bé thì được số lớn nên số lớn gấp \(10\) lần số bé.

- Tìm hai số theo dạng toán tìm hai số khi biết tổng và tỉ số của hai số đó.

Cách giải:

Số lớn nhất có hai chữ số là \(99\) nên tổng của hai số là \(99\).

Viết thêm một chữ số  \(0\) vào bên phải số bé thì được số lớn nên số lớn gấp \(10\) lần số bé, tức là nếu coi số bé gồm \(1\) phần thì số lớn gồm \(10\) phần như thế.

Tổng số phần bằng nhau là:

                  \(1+10=11\) (phần)

Số bé là:

                  \(99:11=9\)

Số lớn là:

                  \(99-9=90\)

                                Đáp số: Số bé: \(9\);

                                            Số lớn: \(90\).

Chọn C.

Câu 2. 

Phương pháp:

- Tìm hiệu giữa chiều dài và chiều rộng: nếu chiều rộng tăng thêm 9m, chiều dài bớt đi 9m thì mảnh đất trở thành hình vuông nên hiệu giữa chiều dài và chiều rộng là: \(9+9 =18m\).

- Tìm chiều dài và chiều rộng theo bài toán tìm hai số khi biết hiệu và tỉ số của hai số đó.

- Tìm diện tích \(=\) chiều dài \(\times\) chiều rộng. 

Cách giải:

Nếu chiều rộng tăng thêm 9m, chiều dài bớt đi 9m thì mảnh đất trở thành hình vuông nên hiệu giữa chiều dài và chiều rộng là:

                       \(9+9 =18\;(m)\)

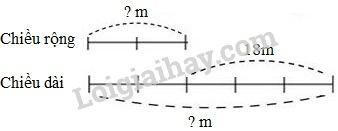
Ta có sơ đồ:

Theo sơ đồ, hiệu số phần bằng nhau là:

                     \(5-2=3\) (phần)

Chiều rộng mảnh đất đó là:

                     \(18:3 \times 2 = 12 \;(m)\)

Chiều dài mảnh đất đó là:

                     \(12  + 18 =30 \;(m)\)

Diện tich mảnh đất đó là:

                     \(30 \times 12 = 360 \;(m^2)\)

                                     Đáp số: \(360m^2.\)

Chọn B.  

Câu 3. 

Phương pháp:

- Đổi:  \(16\) phút \(= \dfrac{16}{60}\) giờ \(= \dfrac{4}{15}\) giờ;

       \(9km \;600m= 9 \dfrac{600}{1000}km =9 \dfrac{3}{5}km= \dfrac{48}{5}km \);

       \(5\dfrac{1}{3}\) giờ \(-\dfrac{16}{3}\) giờ.

- Tìm số ki-lô-mét người đó đi được trong \(1\) giờ ta lấy \(\dfrac{48}{5}\) chia cho \(\dfrac{4}{15}\).

- Tìm số ki-lô-mét người đó đi được trong \(5\dfrac{1}{3}\) giờ ta lấy số ki-lô-mét người đó đi được trong \(1\)  giờ nhân với \(5\dfrac{1}{3}\).

Cách giải: 

Đổi:  \(16\) phút \(= \dfrac{16}{60}\) giờ \(= \dfrac{4}{15}\) giờ;

       \(9km \;600m= 9 \dfrac{600}{1000}km =9 \dfrac{3}{5}km= \dfrac{48}{5}km \);

        \(5\dfrac{1}{3}\) giờ \(\dfrac{16}{3}\) giờ.

Trong \(1\) giờ người đó đi được số ki-lô-mét là:

                   \(\dfrac{48}{5}: \dfrac{4}{15} = 36\;(km)\)

Trong \(\dfrac{16}{3}\) giờ (hay \(5\dfrac{1}{3}\) giờ) người đó đi được số ki-lô-mét là:

                   \( 36 \times \dfrac{16}{3} = 192\;(km)\)

                                                   Đáp số: \(192km.\)

a) S;        b) S;         c) Đ.

Câu 4. 

Phương pháp:

Càng có nhiều người thì số ngày làm xong đoạn đường đó càng ít. Đây là bài toán về quan hệ tỉ lệ.

Để giải bài toán về quan hệ tỉ lệ, ta có thể dùng phương pháp "rút về đơn vị" hoặc phương pháp "tìm tỉ số".

Cách giải:

(Phương pháp rút về đơn vị)

\(1\) người  làm xong đoạn đường đó trong số ngày là:

                      \(5 \times 18 = 90 \) (ngày)

30 người làm xong đoạn đường đó trong số ngày là:

                      \(90:30 =3\) (ngày)

                                      Đáp số: \(3\) ngày.

Chọn B.   

Câu 5. 

Phương pháp:

- Tìm tuổi của mỗi người theo dạng toán tìm hai số khi biết tổng và tỉ số.

- Dựa vào nhận xét: Mỗi năm mỗi người tăng 1 tuổi nên hiệu số tuổi hai mẹ con không thay đổi.

Cách giải:

a) Ta có sơ đồ:

Theo sơ đồ, tổng số phần bằng nhau là:

              \(2+7 =9\) (phần)

Tuổi mẹ hiện nay là:

              \(4 \times 7 = 28\) (tuổi)

Tuổi con hiện nay là:

               \(4 \times 2 = 8\) (tuổi)

b) Mẹ hơn con số tuổi là:

               \(28 - 8 = 20\) (tuổi)

Mỗi năm mỗi người tăng \(1\) tuổi nên hiệu số tuổi hai mẹ con không thay đổi. Vậy khi tuổi mẹ gấp 3 lần tuổi con, mẹ vẫn hơn con 20 tuổi.

Coi tuổi con khi đó gồm \(1\) phần thì tuổi mẹ khi đó gồm \(3\) phần như thế.

Hiệu số phần bằng nhau là:

              \(3-1=2\) (phần)

Tuổi con khi đó là:

              \(20:2 \times 1 = 10\) (tuổi)

Số năm sau để tuổi mẹ gấp 3 lần tuổi con là:

             \(10 - 8 = 2\) (năm)

                                  Đáp số: a) Mẹ: \(28\) tuổi ; con: \(8\) tuổi.

                                               b) \(2\) năm.

Câu 6. 

Phương pháp:

 - Tính số mét vuông tường \(6\) người thợ quét được trong \(1\) giờ ta lấy số mét vuông tưởng \(6\) người thợ quét được trong \(4\) giờ chia cho \(4\).

- Tính số mét vuông tường \(1\) người thợ quét được trong \(1\) giờ ta lấy số mét vuông tưởng \(6\) người thợ quét được trong \(1\) giờ chia cho \(6\).

- Tính số mét vuông tường \(8\) người thợ quét được trong \(1\) giờ ta lấy số mét vuông tưởng \(1\) người thợ quét được trong \(1\) giờ nhân với \(8\).

- Tính số giờ để \(8\) người thợ quét được \(200m^2\) ta lấy \(200\) chia cho số mét vuông tường \(8\) người thợ quét được trong \(1\) giờ.

Cách giải:

Trong \(1\) giờ, \(6\) người thợ quét được số mét vuông tường là:

                \(120 :4 = 30\;(m^2)\)

Trong \(1\) giờ, \(1\) người thợ quét được số mét vuông tường là:

                \(30:6 = 5\;(m^2)\)

Trong \(1\) giờ, \(8\) người quét được số mét vuông tường là:

                 \(5 \times 8 = 40\;(m^2)\)

Vậy \(8\) người thợ quét \(200m^2\) hết số giờ là:

                  \(200:40 = 5\) (giờ)

                                             Đáp số: \(5\) giờ.