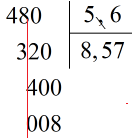Đề số 29 - Đề kiểm tra học kì 1 - Toán lớp 5

Câu 1. Khoanh vào chữ đặt trước câu trả lời đúng:

A. \(8,64:2,4 > \left( {8,64 \times 10} \right):\left( {2,4 \times 10} \right)\)

B. \(8,64:2,4 = \left( {8,64 \times 10} \right):\left( {2,4 \times 10} \right)\)

C. \(8,64:2,4 < \left( {8,64 \times 10} \right):\left( {2,4 \times 10} \right)\)

Câu 2. Đúng ghi Đ, sai ghi S:

a) \(48:5,6 = 8,57\) (dư 8) ☐

b) \(48:5,6 = 8,57\) (dư 0,8) ☐

c) \(48:5,6 = 8,57\) (dư 0,08) ☐

d) \(48:5,6 = 8,57\) (dư 0,008) ☐

Câu 3. Khoanh vào chữ đặt trước câu trả lời đúng:

Điền dấu \(\left( { > , = , < } \right)\)vào chỗ chấm:

\(14,5 : 1,48 \;...\; 1450 : 148\)

A. \(14,5{\rm{ }};{\rm{ }}1,48 > 1450{\rm{ }}:{\rm{ }}148\)

B. \(14,5{\rm{ }};{\rm{ }}1,48 > 1450{\rm{ }}:{\rm{ }}148\)

C. \(14,5{\rm{ }};{\rm{ }}1,48 = 1450{\rm{ }}:{\rm{ }}148\)

Câu 4. Đúng ghi Đ, sai ghi S:

A.

\(36:0,5 > 36 \times 2\)  ☐

\(36:0,5 = 36 \times 2\)  ☐

\(36:0,5 < 36 \times 2\)  ☐

B.

\(72 \times 0,5 > 72:2\)  ☐

\(72 \times 0,5 < 72:2\)  ☐

\(72 \times 0,5 = 72:2\)  ☐

Câu 5. Đúng ghi Đ, sai ghi S:

A.

\(24:0,125 > 24 \times 8\)  ☐

\(24:0,125 < 24 \times 8\)  ☐

\(24:0,125 = 24 \times 8\)  ☐

B.

\(48 \times 0,125 > 48:8\)  ☐

\(48 \times 0,125 = 48:8\)  ☐

\(48 \times 0,125 < 48:8\)  ☐

Câu 6. Tính

\(a)\;7,14:1,5 + 3,06:1,5\)                            \(b)\;9,18:0,5 - 6,12:0,5\)

Câu 7. Tìm \(x\), biết:

\(a)\; x:0,5 + x:0,125 = 9,78\)                      \(b)\; 2,5 \times x \times 6,5 = 152,75\)

Câu 8. Một khu đất hình thoi có diện tích là 229,4m² , có đường chéo thứ nhất bằng 18,5m.

a) Tính độ dài đường chéo thứ hai của khu đất đó.

b) Cạnh khu đất bằng \(\dfrac{3}{4}\) độ dài đường chéo thứ hai. Xung quanh khu đất trồng cây, cây nọ cách cây kia 3,1m. Hỏi phải trồng tất cả bao nhiêu cây?

Câu 1. 

Phương pháp:

Khi nhân số bị chia và số chia với cùng một số khác 0 thì thương không thay đổi.

Cách giải:

Khi nhân số bị chia và số chia với cùng một số khác \(0\) thì thương không thay đổi.

Do đó ta có: \(8,64:2,4 = \left( {8,64 \times 10} \right):\left( {2,4 \times 10} \right)\)

Chọn B.

Câu 2. 

Phương pháp:

Muốn chia một số tự nhiên cho một số thập phân ta làm như sau:

- Đếm xem có bao nhiêu số thập phân ở phần thập phân của số chia thì viết thêm vào bên phải số bị chia bấy nhiêu chữ số \(0.\)

- Bỏ dấu phẩy ở số chia rồi thực hiện phép chia như chia các số tự nhiên.

Cách giải:

Ta đặt tính và thực hiện tính như sau:

Do đó ta có:  \(48:5,6 = 8,57\) (dư 0,008).

Thử lại: \(8,57 \times 5,6 + 0,008 = 48\).

Vậy ta có kết quả như sau:   a) S;          b) S;         c) S;        d) Đ.

Câu 3. 

Phương pháp:

Khi nhân số bị chia và số chia với cùng một số khác 0 thì thương không thay đổi.

Cách giải:

Khi nhân số bị chia và số chia với cùng một số khác \(0\) thì thương không thay đổi.

Do đó ta có: \(14,5 : 1,48= \left( {14,5 \times 100} \right): \) \(\left( {1,48 \times 100} \right)\).

Hay: \(14,5{\rm{ }};{\rm{ }}1,48 = 1450{\rm{ }}:{\rm{ }}148\).

Chọn C

Câu 4. 

Phương pháp:

Tính kết quả các biểu thức rồi so sánh kết quả với nhau.

Cách giải:

A. Ta có:  \(36:0,5 = 72\;\)           \(  36 \times 2=72\).

Mà: \(72 =72\)

Vậy: \(36:0,5 = 36 \times 2\)

Ta có kết quả lần lượt là:    S ;        Đ ;       S.                    

B. Ta có:  \(72 \times 0,5 = 36\;\)           \(  72:2 =36\).

Mà: \(36 =36\)

Vậy: \(72 \times 0,5 = 72:2\)

Ta có kết quả lần lượt là:    S;          S ;      Đ.

Câu 5. 

Phương pháp:

 Tính kết quả các biểu thức rồi so sánh kết quả với nhau.

Cách giải:

A. Ta có:  \(24:0,125 = 192 \) ;          \(24 \times 8=192\)

Mà:  \(192 =192\).

Vậy:   \(24:0,125 = 24 \times 8\)

Ta có kết quả lần lượt là:    S ;         S ;         Đ.                 

B. Ta có: \(48 \times 0,125 =6\)  ;      \(48:8=6\)

Mà:  \(6=6\).

Vậy:  \(48 \times 0,125 = 48:8\).

Ta có kết quả lần lượt là:    S ;         Đ ;         S.

Câu 6.

Phương pháp:

 Áp dụng tính chất chia một tổng hoặc một hiệu cho một số:

\(a:c+b:c = (a+b):c\)  ;        \(a:c-b:c = (a-b):c\)

Cách giải:

a) \(7,14:1,5 + 3,06:1,5\)

    \( = \left( {7,14 + 3,06} \right):1,5\)

    \( = 10,2:1,5 = 6,8\)

b) \(9,18:0,5 - 6,12:0,5\)

    \( = \left( {9,18 - 6,12} \right):0,5\)

    \( = 3,06:0,5 = 6,12\)

Câu 7. 

Phương pháp:

 - Viết phép chia hai số dưới dạng phép nhân hai số.

- Áp dụng tính chất nhân một số với một tổng:   \(a\times (b+c) = a \times b + a\times c\).

- Áp dụng quy tắc: Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.

Cách giải:

a) \(x:0,5 + x:0,125 = 9,78\)

    \(x : \dfrac{1}{2} + x : \dfrac{1}{8} = 9,78\)

    \(x \times 2 + x \times 8 = 9,78\)

    \(x \times \left( {2 + 8} \right) = 9,78\)

    \(x \times 10 = 9,78\)

    \(x = 9,78:10 \)

    \(x= 0,978\)

b) \(2,5 \times x \times 6,5 = 152,75\)

    \(2,5 \times x = 152,75:6,5\)

    \(2,5 \times x = 23,5\)

    \(x = 23,5:2,5 \)

    \( x= 9,4.\)

Câu 8.

Phương pháp:

- Để tính độ dài đường chéo thứ hai ta lấy \(2\) lần diện tích chia cho độ dài đường chéo thứ nhất.

- Tính cạnh khu đất ta lấy  độ dài đường chéo thứ hai nhân với \(\dfrac{3}{4}\).

- Tính chu vi khu đất ta lấy cạnh khu đất nhân với \(4\).

- Tính số cây cần trồng ta lấy chu vi khu đất chia cho khoảng cách giữa hai cây.

Cách giải:

a) Độ dài đường chéo thứ hai của hình thoi là:

                 \(229,4 \times 2:18,5 = 24,8\;(m)\)

b) Cạnh khu đất hình thoi là:

                \(24,8 \times \dfrac{3}{4} = 18,6\;(m)\)

Chu vi khu đất đó là:

                \(18,6 \times 4 = 74,4\;(m)\)

Số cây trồng xung quanh khu đất đó là:

                \(74,4:3,1 = 24\) (cây)

                                      Đáp số: a) \(24,8m\) ;

                                                  b) \(24\) cây.