Đề số 6 - Đề kiểm tra học kì 1 - Toán lớp 5

Câu 1. Khoanh vào chữ số đặt trước câu trả lời đúng:

So sánh \(3\dfrac{2}{5}\) và \(3\dfrac{4}{{10}}\):

A. \(3\dfrac{2}{5} < 3\dfrac{4}{{10}}\)

B. \(3\dfrac{2}{5} > 3\dfrac{4}{{10}}\)

C. \(3\dfrac{2}{5} = 3\dfrac{4}{{10}}\)

Câu 2. Đúng ghi Đ, sai  ghii S:

a) \(2m\;45mm = 2\dfrac{{45}}{{100}}m\)  ☐

b) \(2m\;45mm = 2\dfrac{{45}}{{1000}}m\)  ☐

c) \(8km\;9m = 8\dfrac{9}{{100}}m\)  ☐

d) \(8km\;9m = 8\dfrac{9}{{1000}}km\)  ☐                      

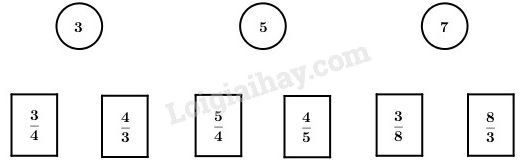
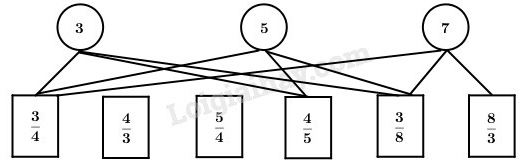
Câu 3. Nối số tự nhiên với phân số để được hỗn số:

Câu 4. Khoanh vào chữ đặt trước câu trả lời đúng:

a) \(5\dfrac{3}{4} = ?\)

A. \(\dfrac{{15}}{4}\)             B. \(\dfrac{{20}}{4}\)               C. \(\dfrac{{23}}{4}\)

b) \(\dfrac{{38}}{3} = ?\)

A. \(12\dfrac{1}{3}\)            B. \(12\dfrac{2}{3}\)             C. \(12\dfrac{3}{4}\)

Câu 5. Đúng ghi Đ, sai  ghi S:

a) \(1\dfrac{3}{4}\) tấn < \(10\dfrac{3}{4}\) tạ  ☐

b) \(1\dfrac{3}{4}\) tấn =\(10\dfrac{3}{4}\) tạ ☐

c) \(1\dfrac{3}{4}\) tấn > \(10\dfrac{3}{4}\) tạ ☐

Câu 6. Tính bằng cách hợp lí nhất:

a) \(1\dfrac{1}{3} \times 1\dfrac{1}{4} \times 1\dfrac{1}{5} \times 1\dfrac{1}{6} \times 1\dfrac{1}{7} \times 1\dfrac{1}{8} = \)

b) \(1\dfrac{1}{3}:1\dfrac{1}{4}:1\dfrac{1}{5}:1\dfrac{1}{6}:1\dfrac{1}{7}:1\dfrac{1}{8} = \)

Câu 7. Có hai vòi nước cùng chảy vào một bẻ không chứa nước. Nếu vòi thứ nhất chaỷ riêng thì sau 9h sẽ đầy bể. Nếu vòi thứ hai chảy riêng thì sau 6 giờ sẽ đầy bể.

Hỏi hai vòi cùng chảy lúc 8 giờ 24 phút thì đến mấy giờ đầy nước?

Câu 8. Tìm a biết a là số tự nhiên:

\(\left( {\dfrac{6}{7} + \dfrac{1}{4}} \right):\left( {\dfrac{{19}}{{14}} - \dfrac{1}{4}} \right) < a < \dfrac{7}{3}\)

Câu 1. 

Phương pháp:

Chuyển hỗn số thành phân số rồi so sánh hai phân số như thông thường.

Cách giải:

Ta có: \(3\dfrac{2}{5}=\dfrac{17}{5}\) ;         \(3\dfrac{4}{{10}}=\dfrac{34}{10}= \dfrac{17}{5}\)

Mà:    \(\dfrac{17}{5}=\dfrac{17}{5}\)

Vậy:   \(3\dfrac{2}{5} = 3\dfrac{4}{{10}}\)

Chọn C. 

Câu 2. 

Phương pháp:

 Dựa vào cách chuyển đổi các đơn vị đo độ dài:

\(1km=1000m\), hay \(1m=\dfrac{{1}}{{1000}}km\) ; 

\(1m=1000mm\), hay \(1mm=\dfrac{{1}}{{1000}}m\).

Cách giải:

+) \(2m\;45mm = 2\dfrac{{45}}{{1000}}m\)

+) \(8km\;9m = 8\dfrac{9}{{1000}}km\)

Vậy ta có đáp án như sau:

a) S;                                     b) Đ; 

c) S;                                     d) Đ.

Câu 3.

Phương pháp:

 Dựa vào tính chất: Phần phân số của hỗn số bao giờ cũng bé hơn đơn vị.

Cách giải:

Câu 4.

Phương pháp:

*) Có thể viết hỗn số thành một phân số có:

- Tử số bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số.

- Mẫu số bằng mẫu số ở phần phân số.

*) Để viết phân số dưới dạng hỗn số ta lấy tử số chia cho mẫu số, thương trong phép chia chính là phần nguyên, phần phân số có tử số là số dư còn mẫu số là mẫu số của phân số ban đầu.

Cách giải:

a)\(5\dfrac{3}{4} = \dfrac{5\times 4 + 3}{4} =\dfrac{{23}}{4}\)

Chọn C.

b) Ta có \(38 : 3 = 12\) dư \(2\) nên \(\dfrac{{38}}{3} = 12\dfrac{2}{3}\)

Chọn B.

Câu 5. 

Phương pháp:

- Đổi hai số đo về cùng đơn vị đo rồi so sánh kết quả với nhau.

- Áp dụng cách đổi: \(1\) tấn \(=10\) tạ.

Cách giải:

Ta có:

+) \(1\dfrac{3}{4}\) tấn \(\dfrac{7}{4}\) tấn \(= \dfrac{70}{4}\) tạ.

(Vì \( \dfrac{7}{4} \times 10 =\dfrac{70}{4})

+) \(10\dfrac{3}{4}\) tạ \(=\dfrac{43}{4}\) tạ.

Mà: \(\dfrac{70}{4}\) tạ \(>\) \(=\dfrac{43}{4}\) tạ

hay \(1\dfrac{3}{4}\) tấn \(>\;10\dfrac{3}{4}\) tạ

Vậy ta có đáp án như sau:

a) S;                         b) S;                     c) Đ.

Câu 6.

Phương pháp:

Đổi hỗn số thành phân số rồi thực hiện phép tính với các phân số như thông thường.

Cách giải:

a) \(1\dfrac{1}{3} \times 1\dfrac{1}{4} \times 1\dfrac{1}{5} \times 1\dfrac{1}{6} \times 1\dfrac{1}{7} \times 1\dfrac{1}{8}\)

\( = \dfrac{4}{3} \times \dfrac{5}{4} \times \dfrac{6}{5} \times \dfrac{7}{6} \times \dfrac{8}{7} \times \dfrac{9}{8}\)

\(=\dfrac{4\times 5\times 6 \times 7 \times 8 \times 9}{3 \times 4\times 5\times 6 \times 7 \times 8 }\)

\( = \dfrac{9}{3} = 3.\)

b) \(1\dfrac{1}{3}:1\dfrac{1}{4}:1\dfrac{1}{5}:1\dfrac{1}{6}:1\dfrac{1}{7}:1\dfrac{1}{8}\)

\( = \dfrac{4}{3}:\dfrac{5}{4}:\dfrac{6}{5}:\dfrac{7}{6}:\dfrac{8}{7}:\dfrac{9}{8}\)

\( = \dfrac{4}{3} \times \dfrac{4}{5} \times \dfrac{5}{6} \times \dfrac{6}{7} \times \dfrac{7}{8} \times \dfrac{8}{9}\)

\(= \dfrac{{4 \times 4\times 5\times 6 \times 7 \times 8}}{{3 \times 5\times 6 \times 7 \times 8\times 9}} \)

\(=\dfrac{4 \times 4}{3 \times 9} =\dfrac{{16}}{{27}}.\)

Câu 7. 

Phương pháp:

- Coi cả bể nước là \(1\) đơn vị.

- Tìm số phần bể nước vòi thứ nhất hoặc vòi thứ hai chảy được trong \(1\) giờ ta lấy \(1\) chia cho số giờ để vòi thứ nhất hoặc vòi thứ hai chảy đầy bể.

- Tính tổng số phần bể nước vòi thứ nhất và vòi thứ hai chảy được trong \(1\) giờ.

- Tìm số giờ để bể đầy nước nếu hai vòi cùng chảy ta lấy \(1\) chia cho tổng số phần bể nước vòi thứ nhất và vòi thứ hai chảy được trong \(1\) giờ.

- Tìm thời gian lúc bể đầy nước ta lấy thời gian lúc hai vòi bắt đầu chảy vào bể cộng với thời gian hai vòi chảy đầy bể

Cách giải:

Trong 1 giờ vòi thứ nhất chảy được số phần bể nước là:

                        \(1:9 = \dfrac{1}{9}\) (bể)

Trong 1 giờ vòi thứ hai chảy được số phần bể nước là:

                        \(1:6 = \dfrac{1}{6}\) (bể)

Trong 1 giờ cả hai vòi chảy được số phần bể nước là:

                       \(\dfrac{1}{6} + \dfrac{1}{9} = \dfrac{5}{{18}}\) (bể)

Thời gian hai vòi chảy đầy bể là:

                        \(1:\dfrac{5}{{18}} = \dfrac{{18}}{5}\)(giờ)

                        \(\dfrac{{18}}{5}\)(giờ) \(= 3\) giờ \(36\) phút

Bể đầy nước lúc:

                       \(8\) giờ \(24\) phút \(+ \;3\) giờ \(36\) phút \(= 12\) giờ

                                                        Đáp số: \(12\) giờ .

Câu 8. 

Phương pháp:

- Tính giá trị ở vế trái rồi từ đó tìm số tự nhiên thích hợp.

- Biểu thức có dấu ngoặc thì ta tính trong ngoặc trước, ngoài ngoặc sau.

Cách giải:

Ta có:

\(\left( {\dfrac{6}{7} + \dfrac{1}{4}} \right):\left( {\dfrac{{19}}{{14}} - \dfrac{1}{4}} \right) \)

\(=\left( {\dfrac{24}{28} + \dfrac{7}{28}} \right):\left( {\dfrac{{38}}{{28}} - \dfrac{7}{28}} \right) \)

\(= \dfrac{{31}}{{28}}:\dfrac{{31}}{{28}}\)     

\(= 1\)

Do đó ta có:  \( 1< a < \dfrac{7}{3}\)

Vì \(a\) là số tự nhiên nên \(a = 2.\)