Đề số 5 - Đề kiểm tra học kì 1 - Toán lớp 5

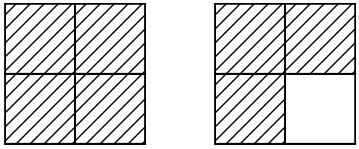
Câu 1. Đúng ghi Đ, sai ghi S vào ô trống bên cạnh hỗn số thích hợp với hình vẽ:

a) \(1\dfrac{1}{2}\) ☐             b) \(1\dfrac{2}{4}\) ☐            c) \(1\dfrac{3}{4}\) ☐

 Câu 2. Khoanh vào chữ đặt trước câu trả lời đúng:

Chuyển hỗn số thành phân số:

A. \(3\dfrac{1}{2} = \dfrac{{3 + 1 + 2}}{2} = \dfrac{6}{2}\)

B. \(3\dfrac{1}{2} = \dfrac{{3 \times 2 + 1}}{2} = \dfrac{7}{2}\)

C. \(3\dfrac{1}{2} = \dfrac{{3 \times 1 + 2}}{2} = \dfrac{5}{2}\)

D. \(3\dfrac{1}{2} = \dfrac{{3 + 2 \times 1}}{2} = \dfrac{5}{2}\)

Câu 3. Đúng ghi Đ, sai ghi S.

a) \(3\dfrac{2}{5} = \dfrac{6}{5}\)  ☐

\(3\dfrac{2}{5} = \dfrac{{15}}{5}\)  ☐ 

\(3\dfrac{2}{5} = \dfrac{{17}}{5}\)  ☐

b) \(5\dfrac{3}{8} = \dfrac{{15}}{8}\)  ☐

\(5\dfrac{3}{8} = \dfrac{{43}}{8}\)  ☐

\(5\frac{3}{8} = \frac{{40}}{8}\)  ☐

Câu 4. Đúng ghi Đ, sai ghi S:

Viết thành hỗn số:

a) \(3m\,7dm = 3\dfrac{7}{{10}}dm\)  ☐

b) \(3m\,7dm = 3\dfrac{7}{{10}}m\)  ☐

c) \(15m\,14cm = 15\dfrac{{14}}{{10}}m\)  ☐

d) \(15m\,14cm = 15\dfrac{{14}}{{100}}m\)  ☐

e) \(2km\,15m = 2\dfrac{{15}}{{1000}}km\)  ☐

g) \(2km\,15m = 2\dfrac{{15}}{{100}}km\)  ☐

Câu 5. Nêu cách chuyển hỗn số thành phân số:

a) \(2\dfrac{3}{7} = ...\)                       b) \(7\dfrac{1}{3} = ...\)

c) \(15\dfrac{{11}}{{14}} = ...\)                d) \(9\dfrac{3}{{125}} = ...\)

Câu 6. Chuyển hỗn số thành phân số rồi thực hiện phép tính:

a)\(4\dfrac{2}{5} + 3\dfrac{1}{{10}} = ...\)

b) \(7\dfrac{3}{8} - 5\dfrac{1}{4} = ...\)

c) \(3\dfrac{2}{9} \times 4\dfrac{3}{5} =...\)

d) \(5\dfrac{2}{3}:4\dfrac{1}{2} = ...\)

Câu 7. Tìm \(x\):

\(x \times 2 + x \times \dfrac{1}{5} = 1\dfrac{3}{5}\)

Câu 8. Một mảnh đất hình chữ nhật có chiều dài \(15\dfrac{1}{2}\)m, chiều rộng \(8\dfrac{1}{3}m\). Tính chu vi và diện tích của mảnh đất đó.

Câu 1. 

Phương pháp:

 Quan sát hình vẽ để tìm hỗn số thích hợp với hình vẽ đã cho.

Cách giải:

Hình vẽ ta cho đã gạch chéo \(1\) hình vuông và \(\dfrac{3}{4}\) hình vuông.

Do đó, hỗn số thích hợp với hình vẽ đã cho là \(1\dfrac{3}{4}\).

Ta có đáp án như sau:

a) S;                                b) S;                               c) Đ.

Câu 2. 

Phương pháp:

 Có thể viết hỗn số thành một phân số có:

- Tử số bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số.

- Mẫu số bằng mẫu số ở phần phân số.

Cách giải:

\(3\dfrac{1}{2} = \dfrac{{3 \times 2 + 1}}{2} = \dfrac{7}{2}\)

Chọn B. 

Câu 3.

Phương pháp:

 Có thể viết hỗn số thành một phân số có:

- Tử số bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số.

- Mẫu số bằng mẫu số ở phần phân số.

Cách giải:

a) \(3\dfrac{2}{5} = \dfrac{{3 \times 5 + 2}}{2}=\dfrac{{17}}{5}\)

Ta có đáp án lần lượt như sau:   S;           S;           Đ.

b) \(5\dfrac{3}{8} = \dfrac{{5 \times 8 + 3}}{8}=\dfrac{{43}}{8}\) 

Ta có đáp án lần lượt như sau:   S;           Đ;           S.

Câu 4.

Phương pháp:

Dựa vào cách chuyển đổi các đơn vị đo độ dài:

\(1km=1000m\), hay \(1m=\dfrac{{1}}{{1000}}km\) ; 

\(1m=10dm\), hay \(1dm=\dfrac{{1}}{{10}}m\) ;

\(1m=100cm\), hay \(1cm=\dfrac{{1}}{{100}}m\) ;

Cách giải:

+) \(3m\;7dm = 3\dfrac{7}{{10}}m\) ; 

+) \(15m\;14cm = 15\dfrac{{14}}{{100}}m\) ; 

+) \(2km\;15m = 2\dfrac{{15}}{{1000}}km\).

Vậy ta có đáp án như sau:

a) S;                       b) Đ;                     c) S;

d) Đ;                       e) Đ;                     g) S.

Câu 5.

Phương pháp:

 Có thể viết hỗn số thành một phân số có:

- Tử số bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số.

- Mẫu số bằng mẫu số ở phần phân số.

Cách giải:

a) \(2\dfrac{3}{7} = \dfrac{{2 \times 7+ 3}}{7}= \dfrac{{17}}{2}\);

b) \(7\dfrac{1}{3} =\dfrac{{7\times 3 + 1}}{3}=\dfrac{{22}}{3}\);

c) \(15\dfrac{{11}}{{14}} =\dfrac{{15 \times 14 + 11}}{14}=\dfrac{{221}}{{14}}\);

d) \(9\dfrac{3}{{125}} = \dfrac{{9 \times 125+ 3}}{125}=\dfrac{{1128}}{{125}}\).

Câu 6.

Phương pháp:

 - Có thể viết hỗn số thành một phân số có:

+) Tử số bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số.

+) Mẫu số bằng mẫu số ở phần phân số.

- Thực hiện các phép tính với phân số nhưng thông thường.

Cách giải:

a) \(4\dfrac{2}{5} + 3\dfrac{1}{{10}} = \dfrac{{22}}{5} + \dfrac{{31}}{{10}} = \dfrac{{44}}{5} + \dfrac{{31}}{{10}}\)\(= \dfrac{{75}}{{10}} = \dfrac{{15}}{2}\) 

b) \(7\dfrac{3}{8} - 5\dfrac{1}{4} = \dfrac{{59}}{8} - \dfrac{{21}}{4} = \dfrac{{59}}{8} - \dfrac{{42}}{8}\) \(= \dfrac{{17}}{8}\)

c) \(3\dfrac{2}{9} \times 4\dfrac{3}{5} = \dfrac{{29}}{9} \times \dfrac{{23}}{5} = \dfrac{{667}}{{45}}\)

d) \(5\dfrac{2}{3}:4\dfrac{1}{2} = \dfrac{{17}}{3}:\dfrac{9}{2} = \dfrac{{17}}{3}\times \dfrac{2}{9}= \dfrac{{34}}{{27}}\)

Câu 7. 

Phương pháp:

 - Áp dụng công thức: \(a \times b + a \times c = a \times (b+c)\).

- Áp dụng quy tắc: Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.

Cách giải:

\(x \times 2 + x \times \dfrac{1}{5} = 1\dfrac{3}{5}\)

\(x \times \left( {2 + \dfrac{1}{5}} \right) = \dfrac{8}{5}\)

\(x \times \dfrac{{11}}{5} = \dfrac{8}{5}\)

\(x = \dfrac{8}{5}:\dfrac{{11}}{5}\)

\(x = \dfrac{8}{{11}}\)

Câu 8. 

Phương pháp:

 Áp dụng các công thức:

- Chu vi \(=\;(\)chiều dài \(+\) chiều rộng \() \;\times \,2)\).

- Diện tích \(=\) chiều dài \(\times \) chiều rộng.

Cách giải:

Đổi:  \(15\dfrac{1}{2}m = \dfrac{{31}}{2}m\,\,; \quad 8\dfrac{1}{3}m = \dfrac{{25}}{3}m\)

Chu vi mảnh đất đó là:

                    \(\left( {\dfrac{{31}}{2} + \dfrac{{25}}{3}} \right) \times 2 = \dfrac{{143}}{3}\;(m)\)

Diện tích mảnh đất đó là: 

                    \(\dfrac{{31}}{2} \times \dfrac{{25}}{3} = \dfrac{{775}}{6}\,({m^2})\)

                                 Đáp số: Chu vi: \(\dfrac{{143}}{3}m;\)

                                              Diện tích: \(\dfrac{{775}}{6}{m^2}.\)